
The eruption of Mt. Pinatubo in the Philippines on June 15, 1991 provided a natural test of the climate system to radiative forcing by producing substantial cooling of global average temperatures over a period of 1 to 2 years. There have been many papers which have studied the event in an attempt to determine the sensitivity of the climate system, so that we might reduce the (currently large) uncertainty in the future magnitude of anthropogenic global warming.
In perusing some of these papers, I find that the issue has been made unnecessarily complicated and obscure. I think part of the problem is that too many investigators have tried to approach the problem from the paradigm most of us have been misled by: believing that sensitivity can be estimated from the difference between two equilibrium climate states, say before the Pinatubo eruption, and then as the climate system responds to the Pinatubo aerosols. The trouble is that this is not possible unless the forcing remains constant, which clearly is not the case since most of the Pinatubo aerosols are gone after about 2 years.
Here I will briefly address the pertinent issues, and show what I believe to be the simplest explanation of what can — and cannot — be gleaned from the post-eruption response of the climate system. And, in the process, we will find that the climate system’s response to Pinatubo might not support the relatively high climate sensitivity that many investigators claim.
Radiative Forcing Versus Feedback
I will once again return to the simple model of the climate system’s average change in temperature from an equilibrium state. Some call it the “heat balance equation”, and it is concise, elegant, and powerful. To my knowledge, no one has shown why such a simple model can not capture the essence of the climate system’s response to an event like the Pinatubo eruption. Increased complexity does not necessarily ensure increased accuracy.
The simple model can be expressed in words as:
[system heat capacity] x[temperature change with time] = [Radiative Forcing] – [Radiative Feedback],
or with mathematical symbols as:
Cp*[dT/dt] = F – lambda*T .
Basically, this equation says that the temperature change with time [dT/dt] of a climate system with a certain heat capacity [Cp, dominated by the ocean depth over which heat is mixed] is equal to the radiative forcing [F] imposed upon the system minus any radiative feedback [lambda*T] upon the resulting temperature change. (The left side is also equivalent to the change in the heat content of the system with time.)
The feedback parameter (lambda, always a positive number if the above equation is expressed with a negative sign) is what we are interested in determining, because its reciprocal is the climate sensitivity. The net radiative feedback is what “tries” to restore the system temperature back to an equilibrium state.
Lambda represents the combined effect of all feedbacks PLUS the dominating, direct infrared (Planck) response to increasing temperature. This Planck response is estimated to be 3.3 Watts per sq. meter per degree C for the average effective radiating temperature of the Earth, 255K. Clouds, water vapor, and other feedbacks either reduce the total “restoring force” to below 3.3 (positive feedbacks dominate), or increase it above 3.3 (negative feedbacks dominate).
Note that even though the Planck effect behaves like a strong negative feedback, and is even included in the net feedback parameter, for some reason it is not included in the list of climate feedbacks. This is probably just to further confuse us.
If positive feedbacks were strong enough to cause the net feedback parameter to go negative, the climate system would potentially be unstable to temperature changes forced upon it. For reference, all 21 IPCC climate models exhibit modest positive feedbacks, with lambda ranging from 0.8 to 1.8 Watts per sq. meter per degree C, so none of them are inherently unstable.
This simple model captures the two most important processes in global-average temperature variability: (1) through energy conservation, it translates a global, top-of-atmosphere radiative energy imbalance into a temperature change of a uniformly mixed layer of water; and (2) a radiative feedback restoring forcing in response to that temperature change, the value of which depends upon the sum of all feedbacks in the climate system.
Modeling the Post-Pinatubo Temperature Response
So how do we use the above equation together with measurements of the climate system to estimate the feedback parameter, lambda? Well, let’s start with 2 important global measurements we have from satellites during that period:
1) ERBE (Earth Radiation Budget Experiment) measurements of the variations in the Earth’s radiative energy balance, and
2) the change in global average temperature with time [dT/dt] of the lower troposphere from the satellite MSU (Microwave Sounding Unit) instruments.
Importantly — and contrary to common beliefs – the ERBE measurements of radiative imbalance do NOT represent radiative forcing. They instead represent the entire right hand side of the above equation: a sum of radiative forcing AND radiative feedback, in unknown proportions.
In fact, this net radiative imbalance (forcing + feedback) is all we need to know to estimate one of the unknowns: the system net heat capacity, Cp. The following two plots show for the pre- and post-Pinatubo period (a) the ERBE radiative balance variations; and (b) the MSU tropospheric temperature variations, along with 3 model simulations using the above equation. [The ERBE radiative flux measurements are necessarily 72-day averages to match the satellite’s orbit precession rate, so I have also computed 72-day temperature averages from the MSU, and run the model with a 72-day time step].
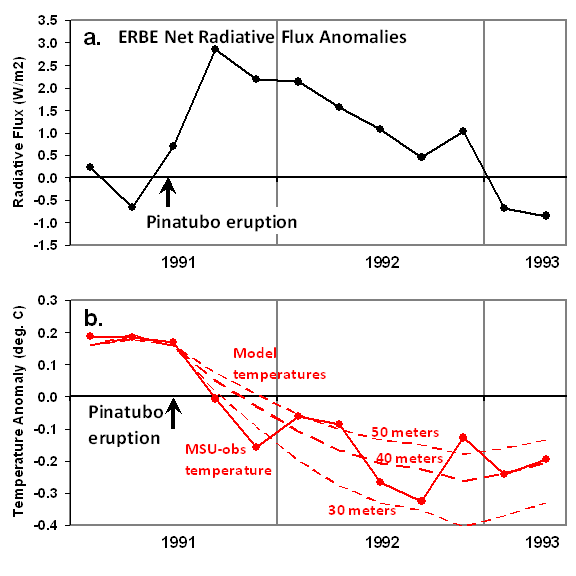
As can be seen in panel b, the MSU-observed temperature variations are consistent with a heat capacity equivalent to an ocean mixed layer depth of about 40 meters.
So, What is the Climate Model’s Sensitivity, Roy?
I think this is where confusion usually enters the picture. In running the above model, note that it was not necessary to assume a value for lambda, the net feedback parameter. In other words, the above model simulation did not depend upon climate sensitivity at all!
Again, I will emphasize: Modeling the observed temperature response of the climate system based only upon ERBE-measured radiative imbalances does not require any assumption regarding climate sensitivity. All we need to know was how much extra radiant energy the Earth was losing [or gaining], which is what the ERBE measurements represent.
Conceptually, the global-average ERBE-measured radiative imbalances measured after the Pinatubo eruption are some combination of (1) radiative forcing from the Pinatubo aerosols, and (2) net radiative feedback upon the resulting temperature changes opposing the temperature changes resulting from that forcing– but we do not know how much of each. There are an infinite number of combinations of forcing and feedback that would be able to explain the satellite observations.
Nevertheless, we do know ONE difference in how forcing and feedback are expressed over time: Temperature changes lag the radiative forcing, but radiative feedback is simultaneous with temperature change.
What we need to separate the two is another source of information to sort out how much forcing versus feedback is involved, for instance something related to the time history of the radiative forcing from the volcanic aerosols. Otherwise, we can not use satellite measurements to determine net feedback in response to radiative forcing.
Fortunately, there is a totally independent satellite estimate of the radiative forcing from Pinatubo.
SAGE Estimates of the Pinatubo Aerosols
For anyone paying attention back then, the 1991 eruption of Pinatubo produced over one year of milky skies just before sunrise and just after sunset, as the sun lit up the stratospheric aerosols, composed mainly of sulfuric acid. The following photo was taken from the Space Shuttle during this time:

There are monthly stratospheric aerosol optical depth (tau) estimates archived at GISS, which during the Pinatubo period of time come from the SAGE (Stratospheric Aerosol and Gas Experiment). The following plot shows these monthly optical depth estimates for the same period of time we have been examining.
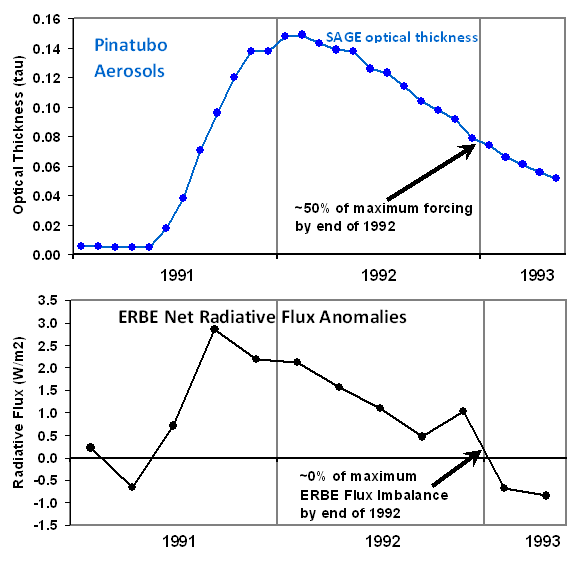
Note in the upper panel that the aerosols dissipated to about 50% of their peak concentration by the end of 1992, which is 18 months after the eruption. But look at the ERBE radiative imbalances in the bottom panel – the radiative imbalances at the end of 1992 are close to zero.
But how could the radiative imbalance of the Earth be close to zero at the end of 1992, when the aerosol optical depth is still at 50% of its peak?
The answer is that net radiative feedback is approximately canceling out the radiative forcing by the end of 1992. Persistent forcing of the climate system leads to a lagged – and growing – temperature response. Then, the larger the temperature response, the greater the radiative feedback which is opposing the radiative forcing as the system tries to restore equilibrium. (The climate system never actually reaches equilibrium, because it is always being perturbed by internal and external forcings…but, through feedback, it is always trying).
A Simple and Direct Feedback Estimate
Previous workers (e.g. Hansen et al., 2002) have calculated that the radiative forcing from the Pinatubo aerosols can be estimated directly from the aerosol optical depths measured by SAGE: the forcing in Watts per sq. meter is simply 21 times the optical depth.
Now we have sufficient information to estimate the net feedback. We simply subtract the SAGE-based estimates of Pinatubo radiative forcings from the ERBE net radiation variations (which are a sum of forcing and feedback), which should then yield radiative feedback estimates. We then compare those to the MSU lower tropospheric temperature variations to get an estimate of the feedback parameter, lambda. The data (after I have converted the SAGE monthly data to 72 day averages), looks like this:
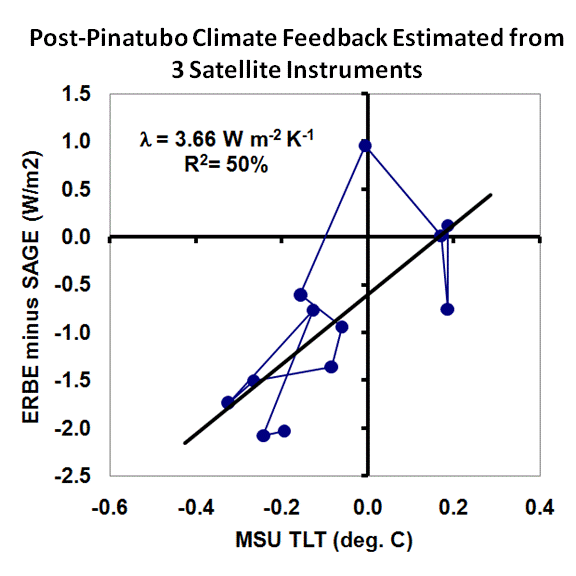
The slope of 3.66 Watts per sq. meter per degree corresponds to weakly negative net feedback. If this corresponded to the feedback operating in response to increasing carbon dioxide concentrations, then doubling of atmosphere CO2 (2XCO2) would cause only 1 deg. C of warming. This is below the 1.5 deg. C lower limit the IPCC is 90% sure the climate sensitivity will not be below.
The Time History of Forcing and Feedback from Pinatubo
It is useful to see what two different estimates of the Pinatubo forcing looks like: (1) the direct estimate from SAGE, and (2) an indirect estimate from ERBE minus the MSU-estimated feedbacks, using our estimate of lambda = 3.66 Watts per sq. meter per deg. C. This is shown in the next plot:
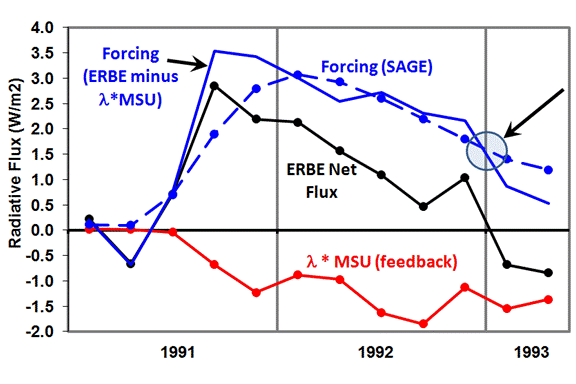
Note that at the end of 1992, the Pinatubo aerosol forcing, which has decreased to about 50% of its peak value, almost exactly offsets the feedback, which has grown in proportion to the temperature anomaly. This is why the ERBE-measured radiative imbalance is close to zero…radiative feedback is canceling out the radiative forcing.
The reason why the ‘indirect’ forcing estimate looks different from the more direct SAGE-deduced forcing in the above figure is because there are other, internally-generated radiative “forcings” in the climate system measured by ERBE, probably due to natural cloud variations. In contrast, SAGE is a limb occultation instrument, which measures the aerosol loading of the cloud-free stratosphere when the instrument looks at the sun just above the Earth’s limb.
Discussion
I have shown that Earth radiation budget measurements together with global average temperatures can not be used to infer climate sensitivity (net feedback) in response to radiative forcing of the climate system. The only exception would be from the difference between two equilibrium climate states involving radiative forcing that is instantaneously imposed, and then remains constant over time. Only in this instance is all of the radiative variability due to feedback, not forcing.
Unfortunately, even though this hypothetical case has formed the basis for many investigations of climate sensitivity, this exception never happens in the real climate system
In the real world, some additional information is required regarding the time history of the forcing — preferably the forcing history itself. Otherwise, there are an infinite number of combinations of forcing and feedback which can explain a given set of satellite measurements of radiative flux variations and global temperature variations.
I currently believe the above methodology, or something similar, is the most direct way to estimate net feedback from satellite measurements of the climate system as it responds to a radiative forcing event like the Pinatubo eruption. The method is not new, as it is basically the same one used by Forster and Taylor (2006 J. of Climate) to estimate feedbacks in the IPCC AR4 climate models. Forster and Taylor took the global radiative imbalances the models produced over time (analogous to our ERBE measurements of the Earth), subtracted the radiative forcings that were imposed upon the models (usually increasing CO2), and then compared the resulting radiative feedback estimates to the corresponding temperature variations, just as I did in the scatter diagram above.
All I have done is apply the same methodology to the Pinatubo event. In fact, Forster and Gregory (also 2006 J. Climate) performed a similar analysis of the Pinatubo period, but for some reason got a feedback estimate closer to the IPCC climate models. I am using tropospheric temperatures, rather than surface temperatures as they did, but the 30+ year satellite record shows that year-to-year variations in tropospheric temperatures are larger than the surface temperatures variations. This means the feedback parameter estimated here (3.66) would be even larger if scaled to surface temperature. So, other than the fact that the ERBE data have relatively recently been recalibrated, I do not know why their results should differ so much from my results.
 |

 Home/Blog
Home/Blog




This piece of writing is really a nice one it helps new web users, who are wishing for blogging.
You gave me even more new perspectives. Your post is very helpful to me. Thank you.