I keep getting dragged into e-mail threads dealing with the claim that climate models (General Circulation Models, or GCMs) don’t even model a spherical Earth….that they apply to a flat Earth where the sun shines 24 hours a day.

I really don’t know where this idea ever came from. It might be because of the Kiehl-Trenberth diagram which illustrates the global-average and time-averaged major energy flows in the climate system, which is often presented over a flat cartoon representation of the Earth’s surface:

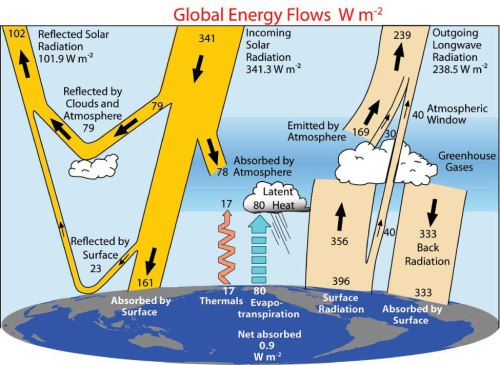
But the 3D computer models of the climate system most assuredly address a spherical, rotating earth, with one side illuminated by the sun.

For example, here’s a YouTube video of one of the GFDL models outgoing infrared radiation, and you can see (1) the land warm and cool during the day/night cycle, as well as (2) rotating weather systems (caused by the Earth’s rotation), and (3) the mid-latitude westerlies which develop in response to the temperature gradients resulting from the curved Earth receiving less sunlight at high latitudes. These are all the result of modeling the system on a spherical, rotating Earth.

Or, if you prefer a map projection that shows the spherical Earth, here’s a different GFDL model showing the ocean surface salinity evolving over time (the model also contains atmospheric circulation systems, which are partly driving the surface currents you see here, but you really can’t effectively visualize more than one or two variables at a time):

(see the very impressive full-res version here).

So, PLEASE, folks…there is plenty to criticize about the climate models. But let’s stick to the stuff that is true, rather than stuff made-up and repeated by people who apparently mistake a cartoon labeled with averages for a full-blown, 3D coupled ocean-atmosphere climate model containing a half-million lines of computer code.

Now, I really loathe having to defend climate models, because I believe they are not yet useful for making climate predictions. But let’s give credit where credit’s due.

The simplest way I’ve found to express climate model shortcomings is this:
Today’s climate models can be tuned to reasonably represent the *average* climate system. But they are, so far, largely useless for what we *really* want to know, that is, how will the climate system change over time?