Home/BlogNOTE: Comments for this post have all been flagged as pending for some reason. I’m testing the spam blocker to see what the problem might be. Until it is fixed, I might have to manually approve comments as I have time during the day.
A recent paper by Jonathan Gregory and co-authors in Climate Dynamics entitled How accurately can the climate sensitivity to CO2 be estimated from historical climate change? addresses in considerable detail the issues which limit our ability to determine that global warming holy grail, “equilibrium climate sensitivity” (ECS, the eventual global average surface warming response to a doubling of atmospheric CO2). Despite decades of research, climate models still exhibit climate sensitivities that range over a factor of three (about 1.5 to 4.5 deg. C for 2XCO2), and a minority of us believe the true sensitivity could be less than 1.5 deg. C.
Obviously, if one could confidently determine the climate sensitivity from observations, then the climate modelers could focus their attention on adjusting their models to reproduce that known sensitivity. But so far, there is no accepted way to determine climate sensitivity from observations. So, instead the climate modeling groups around the world try different approaches to modeling the various physical processes affecting climate change and get a rather wide range of answers for how much warming occurs in response to increasing atmospheric CO2.
One of the problems is that increasing CO2 as a climate forcing is unique in the modern instrumental record. Even if we can measure radiative feedbacks in specific situations (e.g., month to month changes in tropical convection) there is no guarantee that these are the same feedbacks that determine long-term sensitivity to increasing CO2. [If you are one of those who believe the feedback paradigm should not be applied to climate change — you know who you are — you might want to stop reading now to avoid being triggered.]
The Lewis Criticism
The new paper uses climate models as a surrogate for the real climate system to demonstrate the difficulty in measuring the “net feedback parameter” which in turn determines climate sensitivity. While I believe this is a worthwhile exercise, Nic Lewis has objected (originally here, then reposted here and here) to one of the paper’s claims regarding errors in estimating feedbacks through statistical regression techniques. It is a rather obscure point buried in the very long and detailed Gregory et al. paper, but it is nonetheless important to the validity of Lewis and Curry (2018) published estimates of climate sensitivity based upon energy budget considerations. Theirs is not really a statistical technique (which the new paper criticizes), but a physically-based technique applied to the IPCC’s own estimates of the century time scale changes in global radiative forcing, ocean heat storage, and surface temperature change.
From what I can tell, Nic’s objection is valid. Even though it applies to only a tiny portion of the paper, it has significant consequences because the new paper appears to be an effort to de-legitimize any observational estimates of climate sensitivity. I am not questioning the difficulty and uncertainty in making such estimates with current techniques, and I agree with much of what the paper says on the issue (as far as it goes, see the Supplement section, below).
But the authors appear to have conflated those difficulties with the very specific and more physics-based (not statistics-based) climate sensitivity estimates of the Lewis and Curry (2018) paper. Based upon the history of the UN IPCC process of writing its reports, the Gregory et al. paper could now be invoked to claim that the Lewis & Curry estimates are untrustworthy. The fact is that L&C assumes the same radiative forcing as the IPCC does and basically says, the century time scale warming that has occurred (even if it is assumed to be 100% CO2-caused) does not support high climate sensitivity. Rather than getting climate sensitivity from a model that produces too much warming, L&C instead attempt to answer the question, “What is the climate sensitivity based upon our best estimates of global average temperature change, radiative forcing, and ocean heat storage over the last century?”
Vindication for the Spencer and Braswell Studies
I feel a certain amount of vindication upon reading the Gregory et al. paper. It’s been close to 10 years now since Danny Braswell and I published a series of papers pointing out that time-varying radiative forcing generated naturally in the climate system obscures the diagnosis of radiative feedback. Probably the best summary of our points was provided in our paper On the diagnosis of radiative feedback in the presence of unknown radiative forcing (2010). Choi and Lindzen later followed up with papers that further explored the problem.
The bottom line of our work is that standard ordinary least-squares (OLS) regression techniques applied to observed co-variations between top-of-atmosphere radiative flux (from ERBE or CERES satellites) and temperature will produce a low bias in the feedback parameter, and so a high bias in climate sensitivity. [I provide a simple demonstration at the end of this post]. The reason why is that time-varying internal radiative forcing (say, from changing cloud patterns reflecting more or less sunlight to outer space) de-correlates the data (example below). We were objecting to the use of such measurements to justify high climate sensitivity estimates from observations.
Our papers were, of course, widely criticized, with even the editor of Remote Sensing being forced to resign for allowing one of the papers to be published (even though the paper was never retracted). Andrew Dessler objected to our conclusions, claiming that all cloud variations must ultimately be due to feedback from some surface temperature change somewhere at some time (an odd assertion from someone who presumably knows some meteorology and cloud physics).
So, even though the new Gregory et al. paper does not explicitly list our papers as references, it does heavily reference Proistosescu et al. (2018) which directly addresses the issues we raised. These newer papers show that our points were valid, and they come to the same conclusions we did — that high climate sensitivity estimates from the observed co-variations in temperature and radiative flux were not trustworthy.
The Importance of the New Study
The new Gregory et al. paper is extensive and makes many good conceptual points which I agree with. Jonathan Gregory has a long history of pioneering work in feedback diagnosis, and his published research cannot be ignored. The paper will no doubt figure prominently in future IPCC report writing.
But I am still trying to understand the significance of CMIP5 model results to our efforts to measure climate sensitivity from observations, especially the model results in their Fig. 5. It turns out what they are doing with the model data differs substantially with what we try to do with radiative budget observations from our limited (~20 year) satellite record.
First of all, they don’t actually regress top of atmosphere total radiative fluxes from the models against temperature; they first subtract out their best estimate of the radiative forcing applied to those models. This helps isolate the radiative feedback signal responding to the radiative forcing imposed upon the models. Furthermore, they beat down the noise of natural internal radiative and non-radiative variability by using only annual averages. Even El Nino and La Nina events in the models will have trouble surviving annual averaging. Almost all that will remain after these manipulations is the radiative feedback to just the CO2 forcing-induced warming. This also explains why they do not de-trend the 30-year periods they analyze — that would remove most of the temperature change and thus radiative feedback response to temperature change. They also combine model runs together before feedback diagnosis in some of their calculations, further reducing “noise” from internal fluctuations in the climate system.
In other words, their methodology would seem to have little to do with determination of climate sensitivity from natural variations in the climate system, because they have largely removed the natural variations from the climate model runs. The question they seem to be addressing is a very special case: How well can the climate sensitivity in models be diagnosed from 30-year periods of model data when the radiative forcing causing the temperature change is already known and can be subtracted from the data? (Maybe this is why they term theirs a “perfect model” approach.) If I am correct, then they really haven’t fully addressed the more general question posed by their paper’s title: How accurately can the climate sensitivity to CO2 be estimated from historical climate change? The “historical climate change” in the title has nothing to do with natural climate variations.
Unfortunately — and this is me reading between the lines — these newer papers appear to be building a narrative that observations of the climate system cannot be used to determine the sensitivity of the climate system; instead, climate model experiments should be used. Of course, since climate models must ultimately agree with observations, any model estimate of climate sensitivity must still be observations-based. We at UAH continue to work on other observational techniques, not addressed in the new papers, to tease out the signature of feedback from the observations in a simpler and more straightforward manner, from natural year-to-year variations in the climate system. While there is no guarantee of success, the importance of the climate sensitivity issue requires this.
And, again, Nic Lewis is right to object to their implicit lumping the Lewis & Curry observational determination of climate sensitivity work from energy budget calculations in with statistical diagnoses of climate sensitivity, the latter which I agree cannot yet be reliably used to diagnose ECS.
Supplement: A Simple Demonstration of the Feedback Diagnosis Problem
Whether you like the term “feedback” or not (many engineering types object to the terminology), feedback in the climate sense quantifies the level to which the climate system adjusts radiatively to resist any imposed temperature change. This radiative resistance (dominated by the “Planck effect”, the T^4 dependence of outgoing IR radiation on temperature) is what stabilizes every planetary system against runaway temperature change (yes, even on Venus).
The strength of that resistance (e.g., in Watts per square meter of extra radiative loss per deg. C of surface warming) is the “net feedback parameter”, which I will call λ. If that number is large (high radiative resistance to an imposed temperature change), climate sensitivity (proportional to the reciprocal of the net feedback parameter) is low. If the number is small (weak radiative resistance to an imposed temperature change) then climate sensitivity is high.
[If you object to calling it a “feedback”, fine. Call it something else. The physics doesn’t care what you call it.]
I first saw the evidence of the the different signatures of radiative forcing and radiative feedback when looking at the global temperature response to the 1991 eruption of Mt. Pinatubo. When the monthly, globally averaged ERBE radiative flux data were plotted against temperature changes, and the data dots connected in chronological order, it traced out a spiral pattern. This is the expected result of a radiative forcing (in this case, reduced sunlight) causing a change in temperature (cooling) that lags the forcing due to the heat capacity of the oceans. Importantly, this involves a direction of causation opposite to that of feedback (a temperature change causing a radiative change).
The newer CERES instruments provide the longest and most accurate record of changes in top-of-atmosphere radiative balance. Here’s the latest plot for 19 years of monthly Net (reflected shortwave SW plus emitted longwave LW) radiative fluxes versus our UAH lower tropospheric temperatures.
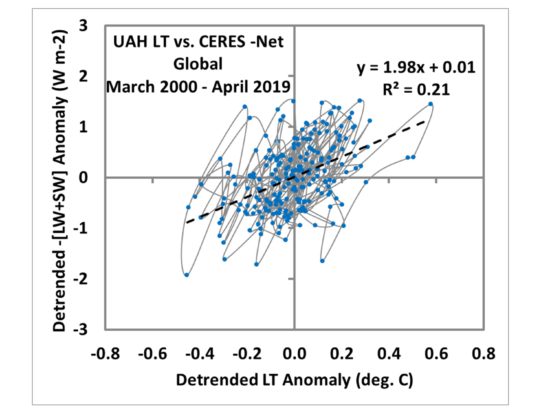
Note I have connected the data dots in chronological order. We see than “on average” (from the regression line) there appears to be about 2 W/m2 of energy lost per degree of warming of the lower troposphere. I say “appears” because some of the radiative variability in that plot is not due to feedback, and it decorrelates the data leading to uncertainty in the slope of the regression line, which we would like to be an estimate of the net feedback parameter.
This contaminating effect of internal radiative forcing can be demonstrated with a simple zero-dimensional time-dependent forcing-feedback model of temperature change of a swamp ocean:
Cp[dT(t)/dt] = F(t) – λ [dT(t)]
where the left side is the change in heat content of the swamp ocean with time, and on the right side F is all of the radiative and non-radiative forcings of temperature change (in W/m2) and λ is the net feedback parameter, which multiplies the temperature change (dT) from an assumed energy equilibrium state.
While this is probably the simplest time-dependent model you can create of the climate system, it shows behavior that we see in the climate system. For example, if I make time series of low-pass filtered random numbers about zero to represent the known time scales of intraseasonal oscillations and El Nino/La Nina, and add in another time series of low-pass filtered “internal radiative forcing”, I can roughly mimic the behavior seen in Fig. 1.
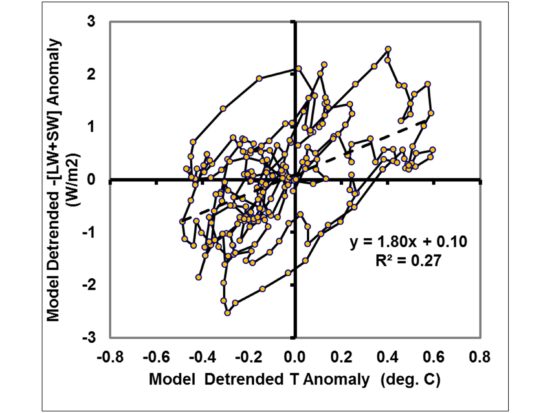
Now, the key issue for feedback diagnosis is that even though the regression line in Fig. 2 has a slope of 1.8 W m-2 K-1, the feedback I specified in the model run was 4 W m-2 K-1. Thus, if I had interpreted that slope as indicating the sensitivity of the simple model climate system, I would have gotten 2. 1 deg. C, when in fact the true specified sensitivity was only 0.9 deg. C (assuming 2XCO2 causes 3.7 W m-2 of radiative forcing).
This is just meant to demonstrate how internal radiative variability in the climate system corrupts the diagnosis of feedback from observational data, which is also a conclusion of the newer published studies referenced above.
And, as I have mentioned above, even if we can diagnose feedbacks from such short term variations in the climate system, we have no guarantee that they also determine (or are even related to) the long-term sensitivity to increasing CO2.
So (with the exception of studies like L&C) be prepared for increased reliance on climate models to tell us how sensitive the climate system is.
CO2 as the climate control knob misses the target completely. I nominate UV intensity as the culprit. Of course, I may be just as wrong as the CO2 huffers.
Lots to study in Gregory et al., which I don’t have time to do just now. At least, the paper is open source for all to read.
There are no climate models.
There are computer games that are called climate models.
The computer games represent the OPINIONS of the team who programmed them.
Since the predictions from the computer games are so far from UAH temperature observations, those opinions are obviously wrong.
Meaning the so-called models are failed prototype models
The climate physics opinions used to build the so-called models have been falsified by inaccurate predictions.
There is no way to estimate ECS until there is a thorough understanding of climate change physics, which would be used as the foundation for a real climate model, that makes accurate predictions.
No such understanding of climate physics exists today.
One could measure the near-global temperature change since 1979, assume rising CO2 is the ONLY cause of the warming, and create a worst case estimate of ECS, which would be about of about 1 — below the low range of the IPCCs wild guess, which has been used since the 1979 Charney Report, and never dies, like a climate zombie..
The only certainty is that man made greenhouse gasses caused anywhere from zero to 100% of the warming since the 1970s.
“Over half” is just a wild guess.
No one can even be certain if the climate will be warmer, or cooler, in 100 years.
Sometimes the smartest climate scientist ‘in the room’ is the one who will admit about ECS that “we don’t know — climate science is far from being settled”.
Some climate models work really well:
https://diggingintheclay.wordpress.com/2014/04/27/robinson-and-catling-model-closely-matches-data-for-titans-atmosphere/
IMO Lewis and Curry have singlehandedly forced the IPCC to lower the bounds of likely ECS (now 1.5 to 4.5), and give up all pretense to “most likely values”…meaning 1.5 is just as likely as any other. In other words they are really confident of very little. It is no surprise at all then that their results must be in someway diminished.
Might I suggest using the EE’s concept of conductance. In this case effective thermal CONDUCTANCE =deltaI/deltaT, where I=radiation power per area(perpendicular to the surface)=Forcing, and T is simply surface or LT temperature. The LW part is the LW (infrared) thermal conductance outward to space, and the SW part is the EFFECTIVE conductance portion due to the change (increase) of cloud SW reflection with temperature. The sum of LW and SW is then just like the parallel connection of 2 different conductors..a simple electrical concept applied to the thermal realm. And it can be easily diagrammed just like an electrical circuit.
In this case a larger conductance decreases the temperature change response to a given forcing change input
ie…deltaT=deltaI/CONDUCTANCE. Then define effective thermal RESISTANCE=1/CONDUCTANCE, so deltaT=deltaI*RESISTANCE…just as in the electrical analog.
To each his own.
My mission is to convince Dr Roy’s faithful flock that rising concentrations of CO2 in the atmosphere are highly beneficial to the environment and to human prosperity.
IMO Lewis and Curry have singlehandedly forced the IPCC to lower the bounds of likely ECS (now 1.5 to 4.5), and give up all pretense to “most likely values”…meaning 1.5 is just as likely as any other. In other words they are really confident of very little. It is no surprise at all then that their results must be in someway diminished.
Might I suggest using the EEs concept of conductance. In this case effective thermal CONDUCTANCE =deltaI/deltaT, where I=radiation power per area(perpendicular to the surface)=Forcing, and T is simply surface or LT temperature. The LW part is the LW (infrared) thermal conductance outward to space, and the SW part is the EFFECTIVE conductance portion due to the change (increase) of cloud SW reflection with temperature. The sum of LW and SW is then just like the parallel connection of 2 different conductors..a simple electrical concept applied to the thermal realm. And it can be easily diagrammed just like an electrical circuit.
In this case a larger conductance decreases the temperature change response to a given forcing change input
iedeltaT=deltaI/CONDUCTANCE. Then define effective thermal RESISTANCE=1/CONDUCTANCE, so deltaT=deltaI*RESISTANCEjust as in the electrical analog.
To each his own.
WordPress censors my response
Please read here:
https://drive.google.com/file/d/1anhvTfWCMUKXsdKyuX5-1G42hQGK3c7F/view?usp=sharing
It’s not that I reject the concept of feedback. It’s that I want it to be applied in accord with the principles of science, not in some invalid way.
The concept of “Feedback” is only meaningful when variables are causally related.
When an amplifier has a voltage gain of 100, applying in input of one Volt implies an output of 100 Volts.
The IPCC climate model (AR5 SPM paragraph D.2) says that the average global temperature is related to the logarithm to the base two of the [CO2].
This is a testable hypothesis that has failed every test. It is safe to assume that CO2 is not causally related to the average global temperature. Consequently it is pointless to discuss “Feedbacks”.
IMO Lewis and Curry have singlehandedly forced the IPCC to lower the bounds of likely ECS (now 1.5 to 4.5), and give up all pretense to “most likely values”…meaning 1.5 is just as likely as any other. In other words they are really confident of very little. It is no surprise at all then that their (L&C) results must be in someway diminished.
Might I suggest using the EE’s concept of conductance. In this case effective thermal CONDUCTANCE =deltaI/deltaT, where I=radiation power per area(perpendicular to the surface)=Forcing, and T is simply surface or LT temperature. The LW part is the LW (infrared) thermal conductance outward to space, and the SW part is the EFFECTIVE conductance portion due to the change (increase) of cloud SW reflection with temperature. The sum of LW and SW is then just like the parallel connection of 2 different conductors..a simple electrical concept applied to the thermal realm. And it can be easily diagrammed just like an electrical circuit.
In this case a larger conductance decreases the temperature change response to a given forcing change input
ie…deltaT=deltaI/CONDUCTANCE. Then define effective thermal RESISTANCE=1/CONDUCTANCE, so deltaT=deltaI*RESISTANCE…just as in the electrical analog.
To each his own.
m d mills,
I like the parallel circuit analogy. I’ve thought about it many times. Think about it… if each 100ppm represents a resistor, how much will changing 1 out of 10,000 resistors by X% really matter? Even if you take that 10,000th resistor completely out and make it an open circuit, you still have 9,999 other ways for the atmosphere to transfer energy, and like a circuit, the current will divide into the remaining resistors. Additional heat produced is unbelievably small. Anyways, I don’t think CO2 is a perfect insulator. You can be fair and say that perhaps it might block around 39% of the energy, but even then, forcing from the sun becomes an order of magnitude+ more important then CO2.
Clearly we need to understand water vapor, clouds and their impact on our climate. That is the main driver right there. Who would have thought that sun and clouds control our climate? lol
Meanwhile, it is snowing in northern Texas. Frost in New Mexico. The temperature over the Great Lakes will drop below 0 C.
How were temperatures in Poland from Oct 12 to Oct 22?
Test
So it looks like random fluctuations on the Temperature axis will always reduce the slope of the regression. Instead of random, if you have a high frequency temperature variation, I assume you would see the same effect. How long do we need to average observations before a signal would emerge?
The earth is in radiative equilibrium at all times, no feedbacks. However, the earth is never in thermodynamic equilibrium characterizing the inert matter becaus the size of life in the biosphere constantly changes.
Dr Spencer
As one would expect, the detrended data plotted in Fig 1 and Fig 2 are behaving as if the forcing/temperature ratio, the sensitivity, was a strange attractor, ie a physically preferred value around which the data oscillates.
When you calculate a trend line from the data, you get a forcing sensitivity of about 2W/m^2/C.
This is twice the IPCC estimate of 3.7W/m^2/C.
Yet you are advocating a very low forcing sensitivty compared to the IPCC estimate, perhaps half the mid-range value.
Have I missed something?
“But so far, there is no accepted way to determine climate sensitivity from observations.”
And there never will be. The climate is always changing, and these natural changes in climate will make it impossible to determine the true influence of increased CO2 concentrations.
If we assume the climate was perfect and unchanging around 1850, and that the climate would still be exactly the same today had we not emitted any additional CO2 into the atmosphere… then the ECS would be (3.3C +/-0.1) using the observations. Wouldn’t it be great if the climate was that simple?
Dr. Roy said:
“From what I can tell, Nics objection is valid. Even though it applies to only a tiny portion of the paper, it has significant consequences because the new paper appears to be an effort to de-legitimize any observational estimates of climate sensitivity.”
While Dr. Roy is awesome in his defense of real science he is not right 100% of the time.
I can’t understand how anyone as smart as Dr. Roy still thinks that the “Sensitivity Constant” is meaningful.
If the sensitivity constant meant anything, global temperature and the concentration of CO2 in the atmosphere would correlate over all time scales.
In reality there is no correlation on any time scale except from 1850 to 1934 and from 1972 to 1998. The IPCC used these coincidental correlations to generate a fake science bubble that depends on “Groupthink”.
https://www.thegwpf.org/content/uploads/2018/02/Groupthink.pdf
Bubbles like this always burst. Let us hope it will be soon as we are wasting $1.5 trillion/year on “Carbon Mitigation” and “Renewables” that make no sense.
What if climate sensitivity isn’t static, but dynamic? Maybe it starts out low at maybe 0.5C per W/m^2 but as the climate system gets more or more perturbed from its semi-stable state the sensitivity increases to 1.0C per W/m^2?
” Thus, if I had interpreted that slope as indicating the sensitivity of the simple model climate system, I would have gotten 2. 1 deg. C, when in fact the true specified sensitivity was only 0.9 deg. C ”
Thanks for your interest in this topic Dr Spencer but sadly you are for some reason missing key problem in this whole Rad vs T regression game.
The reason for the incorrect OLS result is regression dilution, not the decorrelation ( which is a separate legitimate concern ).
It can be seen by eye that the above slopes are WRONG. Do the regression with Rad on abscissa and you get a new totally wrong result biased in the other direction. This is not new. See my article on misuse of OLS on Climate Etc. where I site your papers.
https://judithcurry.com/2016/03/09/on-inappropriate-use-of-least-squares-regression/
The Lewis and Curry method is an attempt not only to use observations but to use a method which does not suffer regression dilution and produce known-to-be false results.
Also it is not correct to call Lewis-Curry method “non statistical” just because it does not (mis)use the sacred OLS. They take decadal averages to remove noise before determining rad/T ratio, instead of incorrectly applied OLS. Thus they are using a non-biases statistical method.
With respect to your decorrelation problem I have suggested a method to tackle this again on Climate Etc.
https://judithcurry.com/2015/02/06/on-determination-of-tropical-feedbacks/
Hopefully the spam filter problem may mean you get to notice this comment. I hope those links will be useful to you. I would like your thoughts on the decorrelation problem.
best regards. Greg.
Appendix D of the Gregory et al paper also explains regression dilution well. It unfortunate that they incorrectly conclude this applies to the difference method, as Nic Lewis points out.
I’d like to see how their ECS from the 1870’s fits in. Global temperature records start in 1880. There’s a lot of evidence that shows a GLOBAL, positive (warm) ocean oscillation in at least 4 different ocean surface temperature proxies spread across the oceans (PDO, AMO, IOD, and NAO) that caused a global land surface catastrophe that has never been seen since (that I know of). If they are willing to stick their necks out there on their overall GCM project, then they should be able to justify the cause of the extreme 1870’s that caused 30 to 60 million deaths.
https://betdoithuong.com/game-bai-doi-thuong/hu86club-cong-game-bai-doi-thuong-xanh-chin-nhat-hanh-tinh
Thị trường game bi ăn tiền ngy cng pht triển, số lượng sn chơi đnh bi mọc ln nhiều như nấm
But so far, there is no accepted way to determine climate sensitivity from observations.