NOTE: This has been revised since finding an error in my analysis, so it replaces what was first published about an hour ago.

As part of an e-mail discussion on climate sensitivity I been having with a skeptic of my skepticism, he pointed me to a paper by Tung & Camp entitled Solar-Cycle Warming at the Earth’s Surface and an Observational Determination of Climate Sensitivity.

The authors try to determine just how much warming has occurred as a result of changing solar irradiance over the period 1959-2004. It appears that they use both the 11 year cycle, and a small increase in TSI over the period, as signals in their analysis. The paper purports to come up with a fairly high climate sensitivity that supports the IPCC’s estimated range, which then supports forecasts of substantial global warming from increasing greenhouse gas concentrations.

The authors start out in their first illustration with a straight comparison between yearly averages of TSI and global surface temperatures during 1959 through 2004. But rather than do a straightforward analysis of the average solar cycle to the average temperature cycle, the authors then go through a series of statistical acrobatics, focusing on those regions of the Earth which showed the greatest relationship between TSI variations and temperature.

I’m not sure, but I think this qualifies as cherry picking — only using those data that support your preconceived notion. They finally end up with a fairly high climate sensitivity, equivalent to about 3 deg. C of warming from a doubling of atmospheric CO2.

Tung and Camp claim their estimate is observationally based, free of any model assumptions. But this is wrong: they DO make assumptions based upon theory. For instance, it appears that they assume the temperature change is an equilibrium response to the forcing. Just because they used a calculator rather than a computer program to get their numbers does not mean their analysis is free of modeling assumptions.

But what bothers me the most is that there was a much simpler, and more defensible way to do the analysis than they presented.

A Simpler, More Physically-Based Analysis

The most obvious way I see to do such an analysis is to do a composite 11-year cycle in TSI (there were 4.5 solar cycles in their period of analysis, 1959 through 2004) and then compare it to a similarly composited 11-year cycle in surface temperatures. I took the TSI variations in their paper, and then used the HadCRUT3 global surface temperature anomalies. I detrended both time series first since it is the 11 year cycle which should be a robust solar signature…any long term temperature trends in the data could potentially be due to many things, and so it should not be included in such an analysis.

The following plot shows in the top panel my composited 11-year cycle in global average solar flux, after applying their correction for the surface area of the Earth (divide by 4), and correct for UV absorption by the stratosphere (multiply by 0.85). The bottom panel shows the corresponding 11-year cycle in global average surface temperatures. I have done a 3-year smoothing of the temperature data to help smooth out El Nino and La Nina related variations, which usually occur in adjacent years. I also took out the post-Pinatubo cooling years of 1992 and 1993, and interpolated back in values from the bounding years, 1991 and 1994.

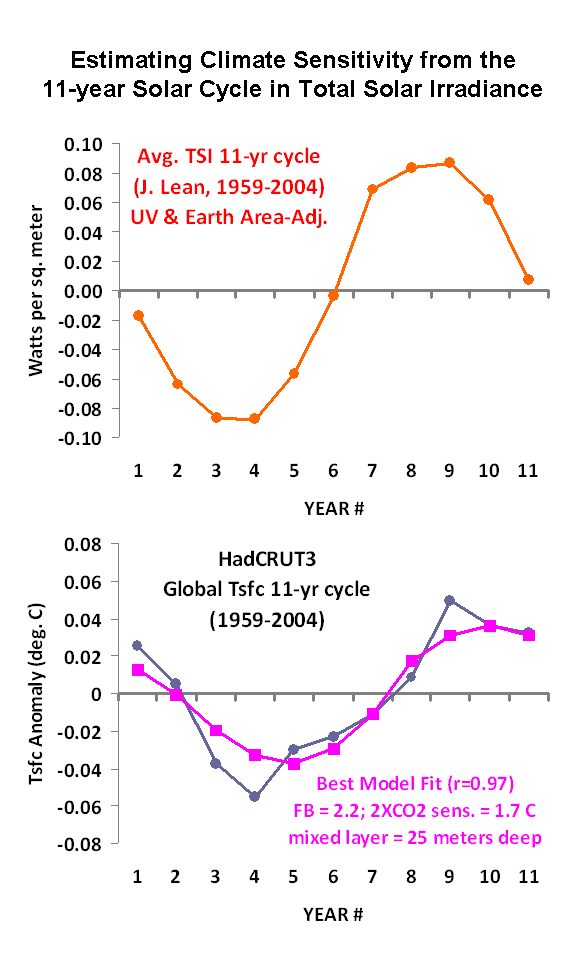
Note there is a time lag of about 1 year between the solar forcing and the temperature response, as would be expected since it takes time for the upper ocean to warm.

It turns out this is a perfect opportunity to use the simple forcing-feedback model I have described before to see which value for the climate sensitivity provides the best fit to the observed temperature response to the 11-year cycle in solar forcing. The model can be expressed as:

Cp[dT/dt] = TSI – lambda*T,

Where Cp is the heat capacity of the climate system (dominated by the upper ocean), dT/dt is the change in temperature of the system with time, TSI represents the 11 year cycle in energy imbalance forcing of the system, and lambda*T is the net feedback upon temperature. It is the feedback parameter, lambda, that determines the climate sensitivity, so our goal is to find a value for a best value for lambda.

I ran the above model for a variety of ocean depths over which the heating/cooling is assumed to occur, and a variety of feedback parameters. The best fits between the observed and model-predicted temperature cycle (an example of which is shown in the lower panel of the above figure) occur for assumed ocean mixing depths around 25 meters, and a feedback parameter (lambda) of around 2.2 Watts per sq. meter per deg. C. Note the correlation of 0.97; the standard deviation of the difference between the modeled and observed temperature cycle is 0.012 deg. C

My best fit feedback (2.2 Watts per sq. meter per degree) produces a higher climate sensitivity (about 1.7 deg. C for a doubling of CO2) than what we have been finding from the satellite-derived feedback, which runs around 6 Watts per sq. meter per degree (corresponding to about 0.55 deg. C of warming).

Can High Climate Sensitivity Explain the Data, Too?

If I instead run the model with the lambda value Tung and Camp get (1.25), the modeled temperature exhibits too much time lag between the solar forcing and temperature response….about double that produced with a feedback of 2.2.

Discussion

The results of this experiment are pretty sensitive to errors in the observed temperatures, since we are talking about the response to a very small forcing — less than 0.2 Watts per sq. meter from solar max to solar min. This is an extremely small forcing to expect a robust global-average temperature response from.

If someone else has published an analysis similar to what I have just presented, please let me know…I find it hard to believe someone has not done this before. I would be nice if someone else went through the same exercise and got the same answers. Similarly, let me know if you think I have made an error.

I think the methodology I have presented is the most physically-based and easiest way to estimate climate sensitivity from the 11-year cycle in solar flux averaged over the Earth, and the resulting 11-year cycle in global surface temperatures. It conserves energy, and makes no assumptions about the temperature being in equilibrium with the forcing.

I have ignored the possibility of any Svensmark-type mechanism of cloud modulation by the solar cycle…this will have to remain a source of uncertainty for now.

The bottom line is that my analysis supports a best-estimate 2XCO2 climate sensitivity of 1.7 deg. C, which is little more than half of that obtained by Tung & Camp (3.0 deg. C), and approaches the lower limit of what the IPCC claims is likely (1.5 deg. C).