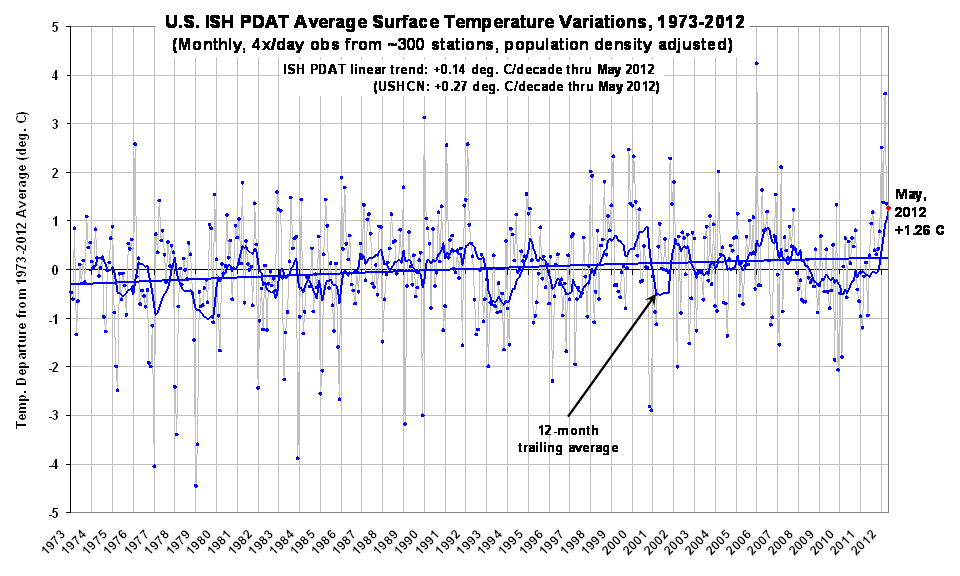
The U.S. lower-48 surface temperature anomaly from my population density-adjusted (PDAT) dataset was 1.26 deg. C above the 1973-2012 average for May 2012, with a 1973-2012 linear warming trend of +0.14 deg. C/decade (click for full-size version):

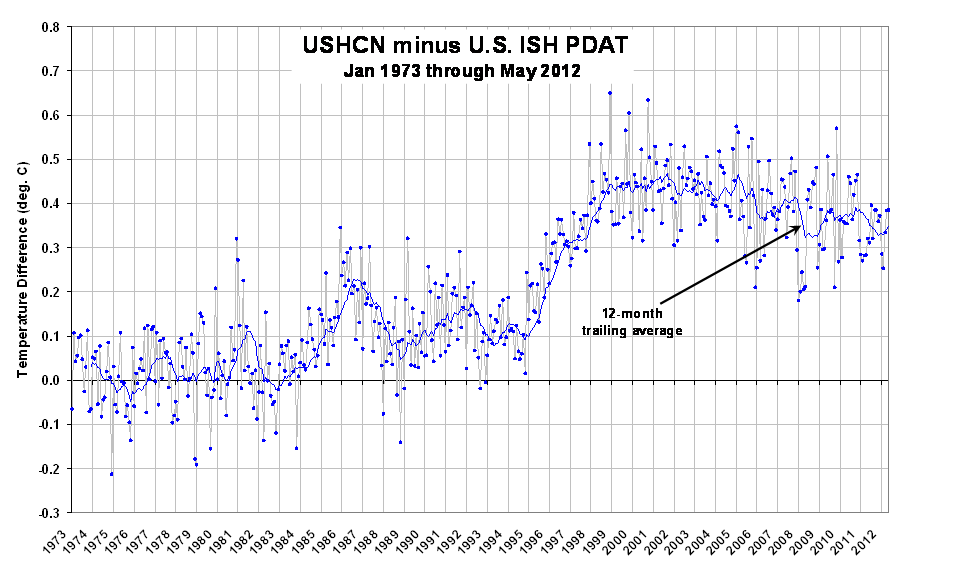
The corresponding USHCN anomaly computed relative to the same base period was +1.65 deg. C, with nearly double my warming trend (+0.27 deg. C/decade). The warming of the USHCN relative to my dataset shows that most of the discrepancy arises during the 1996-98 period:

Despite the weaker warming trend in my dataset, Spring 2012 still ranks as the warmest spring since the beginning of my record (1973). The 12-month period ending in May 2012 is also the warmest 12-month period in the record.

Due to a lack of station data and uncertainties regarding urban heat island (UHI) effects, I have no opinion on how the recent warmth compares to, say, the 1930s. There is also no guarantee that my method for UHI adjustment since 1973 has done a sufficient job of removing UHI effects. A short description of the final procedure I settled on for population density adjustment of the surface temperatures can be found here.