There seems to be continuing confusion regarding how the deep ocean can warm without an observable temperature increase at the ocean surface.
I’m not talking about a change in the geothermal heat flux at the bottom of the ocean. And I’m not claiming Kevin Trenberth is right that this has actually happened in recent years. I’m just pointing out that it is theoretically possible.
The average state of the ocean, except at the highest latitudes, is warm water over cold water. So, there is normally a vertical temperature gradient, which is strongest in the tropics. I won’t go into the various processes which maintain this gradient, but if any one of those processes changes, the vertical temperature gradient can change.
For example, if there was an increase in vertical mixing alone in the ocean, the gradient would be reduced, with surface cooling and deep ocean warming.
Now, what if this increase in vertical mixing occurred at the same time as an additional surface heat source, such as IR warming due to increasing greenhouse gases? The result (conceivably) could be deep ocean warming with no surface warming, as shown in the following cartoon:
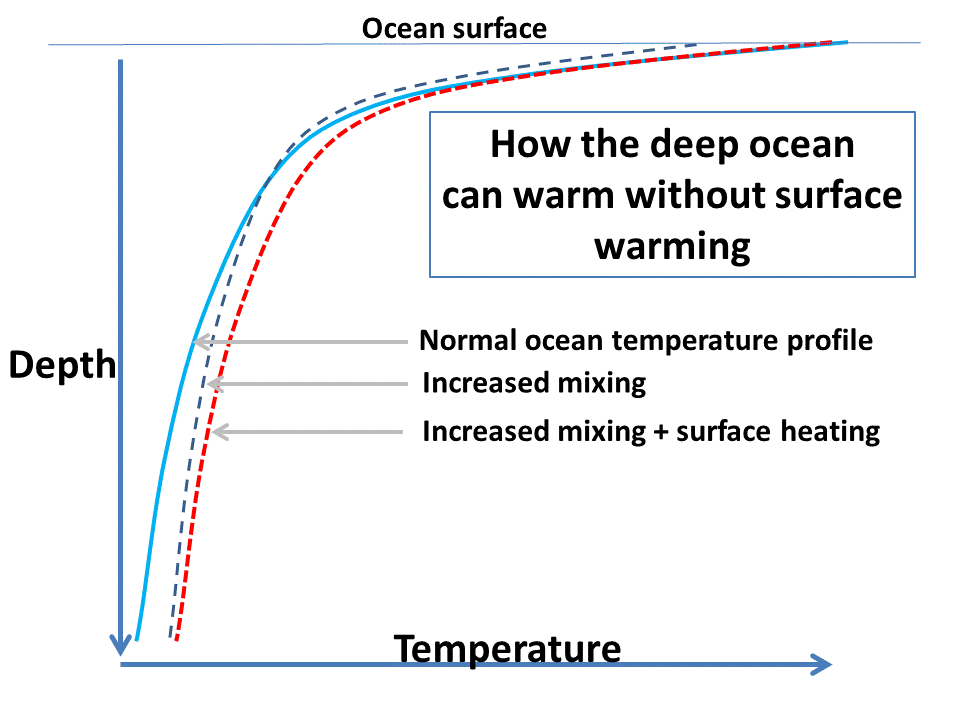
Deep ocean warming can seemingly bypass the surface if surface heating is combined with increased vertical mixing.
As I have posted previously, there was indeed a tiny (2%) increase in global average ocean surface winds after 1997-98 super El Nino, which seems to have recently gone away. Ocean mixing is a complicated subject, and I have no idea whether this small change in ocean winds, if real, is sufficient to cause the “Trenberth effect”.
The extra Joules didn’t actually bypass the surface layer…they were matched by a decrease in Joules extracted from the increased vertical mixing. Temperature change is the net result of a variety of energy gains and losses, and those energy fluxes can change with depth.
And for those wondering how IR heat flux, which only affects the skin of the ocean surface, can affect the deep ocean: the same is true of evaporation, which we know is a major component of the ocean’s energy budget.

 Home/Blog
Home/Blog



