Home/BlogThis is a followup to my post from yesterday where I provided time-dependent model results of the day-night cycle in lunar temperatures.
One of the fascinating things about the model result (which I would not have expected) is that all other things being equal, the faster a solar-illuminated planet rotates, the warmer its average temperature will be. The calculations I provided are for planets without an atmosphere (e.g. the Moon).
Before examining the issue, I would have guessed that the rotation rate would not matter. Or, maybe I would have guessed that a more-slowly rotating planet would get warmer, since the period of sunlight is longer and higher daytime temperatures would be achieved.
But I would have been wrong.
Simple Thought Experiment
The reason is very simple, and is related to the non-linearity of the Stefan-Boltzmann equation, which can be used to estimate how warm a body gets based upon the rate at which it absorbs solar energy when its only mechanism to cool is through thermal emission of radiation:
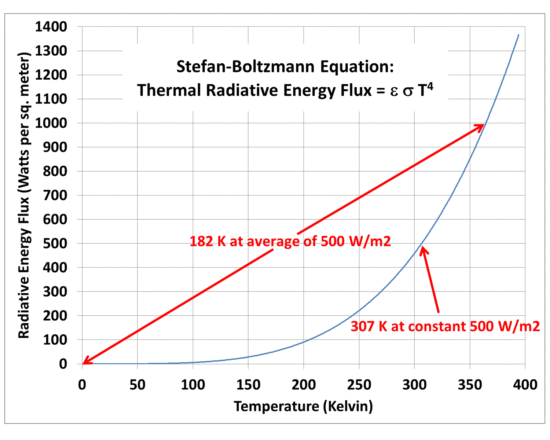
Fig. 1. The non-linearity of the Stefan-Boltzmann equation can lead to very different average planetary temperatures given the same long-term average absorbed solar flux.
Imagine a body with a realistic heat capacity that uniformly absorbs a solar intensity of 1,000 Watts per sq. meter for 1 second, then 0 W/m2 for one second, over and over. Think of it as a 2 sec long diurnal cycle. That rapidly flickering energy source would be too fast for the temperature to come into equilibrium with the absorbed sunlight (or lack of sunlight). It would, in effect, be like a continuous energy source of 500 W/m2 in intensity, and the resulting S-B temperature (assuming a thermal radiative emissivity of 1.0) would be about 307 Kelvin, taken from the curve in Fig. 1.
Now imagine the energy source stays on for a very long time, say 10,000 days, then stays off for 10,000 days (a 20,000 day diurnal cycle…the Moon has a 29.5 day diurnal cycle). From Fig. 1 we see that during the daytime the temperature would approach 365 Kelvin, and at night it would approach 0 Kelvin. In this case the average temperature would be about 182 Kelvin…which is 125 deg. colder than 307 K!
The only difference in the two imaginary cases is the length of the day/night cycle. The long-term average rate of absorbed sunlight is the same.
Yesterday I showed that the difference in rotation rate between the Earth and the Moon caused the more-slowly rotating Moon to be about 55 deg. colder than the Earth, all other things being equal (no atmosphere, the same albedo and IR emissivity, and a surface bulk heat capacity which gives model temperatures than match actual lunar observations). The effect is muted the greater the surface bulk heat capacity, since that also reduces the diurnal temperature range.
Basically, any process which increases the day-night temperature range (such as a longer diurnal cycle) will decrease the average temperature of a planet, simply because of the non-linearity of the S-B equation. I suspect the effect does not exist if the surface being heated has zero heat capacity, since the temperature of the surface will instantly come into equilibrium with the absorbed sunlight; in that case the length of day would not matter. But since that is physically impossible, it does not apply to real planets.
People who drink coffee with cream understand that if they want to keep their coffee warm for the longest period of time, the quicker they add the cream, the better. This is a much more important result of the non-linearity of the Stefan-Boltzmann equation! 😉
Also, did you know that if you balance an ice cube on end during the equinox, it will burst into steam?
Subsurface Temperatures
Heat flow measurements made during the Apollo 15 and 17 missions revealed that the top 1-2 cm of lunar regolith has extremely low thermal conductivity. The mean temperature measured 35cm below the surface of the Apollo sites was 40-45K warmer than the surface. At a depth of 80cm the day/night temperature variation experienced at the surface was imperceptible. This implies that habitations in the lunar subsurface exist that are not subject to the harsh temperature extremes prevalent on the surface.
http://www.diviner.ucla.edu/science
Ren, the subsurface temperature is supported by the surface fluxes. There is no other significant heat source. The regolith is a natural integrator; a physical integrator of the supportive balance at the surface. It indicates that the weighting of the physical temperatures at the surface is calculated incorrectly. Calculated incorrectly by over 40 deg due to a lack of respect for the fact that the mean temperature assigned to the lunar surface ‘must’ satisfy flux balance to be of any value. That temperature is 273K if the values of albido and emissivity are correct.
Geoff, maybe you didn’t read my post from yesterday…the actual global average lunar temperature is more like 210-215K. You can’t compute it from an average absorbed solar flux put through the S-B equation, due to the nonlinearity.
Hi Roy. Fluxes balance not temperatures at eqm, as you know. Assigning 215K to the entire sphere that represents the moon cannot radiate to space the energy absorbed from the solar flux. Nothing like it in fact. Weighting has to be towards the higher temperatures as these are responsible for the bulk of the radiation, due to Holder’s inequality and the non-linearity. We are both talking about the same thing sir.
Yes. And as I said, as a result of that nonlinearity, the resulting global average lunar temperature ends up being about 210-215 K. Not 273 K.
215K emits 115W/m-2 at ε=0.95. The solar flux divided by four is 300W/m-2
Geoff, you seem to be missing the point, even though you yourself raised it (Holders Inequality and nonlinearity). The GLOBAL AVERAGE lunar temperature is 215 K. But the FULL RANGE of temperatures making up the global average are from below 100 K to almost 400K. When you compute the thermally emitted radiative flux at all of those different temperatures and average them over the sphere, they match the absorbed solar flux….and also correspond to the same radiated flux as a moon with a uniform temperature of 273 K. -Roy
So we agree that the flux balancing temperature required is 273K.
How do you explain the higher temperatures measured below the surface?
Barring some geothermal heat source, subsurface temperatures should, on average, reflect the time-averaged surface temperature for that location….just damped with depth. If they are getting something substantially different from that, then their measurements are incomplete or inaccurate. -Roy
You convert temperatures to fluxes, average fluxes then convert back to temperature. That gives a temperature representative of the equilibrium requisite that fluxes balance at eqm.
Not sure what you are saying…I used the latitudinal and diurnally varying absorbed solar flux to compute diurnal temperature variations for a surface with finite heat capacity, all of which impact the resulting temperature. Then compute the global area-average temperature from that.
Many different global temperature distriubutions can balance the same global average absorbed solar flux. Did you read yesterday’s post? It’s very brief and easy to understand.
Roy, with respect, I am saying that 215K as a single number to represent the moon does not satisfy the required flux balance at equilibrium. 273K assigned to every square metre of the lunar surface exactly radiates to space the same as the absorbed flux. Unless the albedo is wrong or the emissivity of lunar rock is wrong that is its temperature.
Ugh…Geoff, I never said the moon has a uniform temperature of 215 K. I said it had an AREA AVERAGE of 215 K…please look at my italicized comments above. You are assuming I said something which I didn’t say. -Roy
If you descend into a cave on Earth you see temperatures that are representative of the physical average of surface variations as they affect physical matter. As you descend the daily, monthly, annual, multidecadal averages are represented. They are a true physical average if the surface supportive fluxes. The mismatch on the moon should have alarm bells ringing that matter doesn’t understand the scientists’ averaging.
And this average, 215K, Roy, although it is an average, has no useful meaning.
I have read that at the equator, 1m into the regolith the temperature is a constant 293K. Sufficient to support a lunar base without heating or cooling and based upon thermometer readings. Diviner area weighted surface readings at the equator are
206K. Of what use is the area weighted calculation if a useable environment exists at a completely different temperature to that calculated?
They should be able to pick a location for a partially-buried lunar base by just knowing what the time averaged surface temperature is. At a sufficient depth, the temperature at depth should match the time-averaged surface temperature. -Roy
Perhaps you are highlighting here, as you believe in a strong radiative influence here on Earth that polar temperature variation is dwarved by miniscule variations in equatorial temperatures as these answer to space mostly, due to non-linearity of flux to temperature? But area weighted is a different ‘story’.
Does this explain the discrepancy between the Diviner ‘measured’ average of 206K and the thermometer in the regolith of greater than 273K at the equator?
It is an embarrassing discrepancy!
And again you have highlighted that the inequality is not just spatial, but temporal as well!
Can you tell me exactly what the discrepancy is? I really doubt one exists.
The subsurface temperature is 40 plus degrees higher than the ‘measured’ surface temperature despite the fact that the subsurface is supported by the mean of surface fluxes!!
And that is the mean discrepancy of an abused non linear spatial and temporal function
Barring some geothermal heat source, subsurface temperatures should, on average, reflect the time-averaged surface temperature for that location.just damped with depth. If they are getting something substantially different from that, then their measurements are incomplete or inaccurate. -Roy
Diviner. From their website, copy and paste,
“Heat flow measurements made during the Apollo 15 and 17 missions revealed that the top 1-2 cm of lunar regolith has extremely low thermal conductivity. The mean temperature measured 35cm below the surface of the Apollo sites was 40-45K warmer than the surface. At a depth of 80cm the day/night temperature variation experienced at the surface was imperceptible. This implies that habitations in the lunar subsurface exist that are not subject to the harsh temperature extremes prevalent on the surface.”
Roy, with respect sir, we are exactly back at my first response tonight .
Did they have a sufficiently long dataset to average out the diurnal variations? The thermal conductivity of the surface shouldn’t matter…that just affects the time to respond. The subsurface should average the same as the surface over a diurnal cycle. Sounds like it’s time to send an email to a few of these people for clarification.
Ive already mailed them. They didn’t want to talk to me.
That’s weird.
I love your sense of humour.-)
I’m going to try emailing those folks anyway. Ya gotta suck up to them. 😉
It affects the time to respond and the depth required to provide a useful integration. Once you are deep enough to see no variation occurring you are deep enough. Anyway modelling at this thermal conductivity confirms results. And you like modelling. Site it down now but here is the link,
http://biocycle.atmos.colostate.edu/shiny/Moon/
Depth should not change the fact that the time averaged temperature should be the same as at the surface. Do you agree?
100% on that Roy
Except that it’s the flux balancing effective mean temperature at the surface. Not a simple average.
One that upholds the non linearity of radiative potential as a function of temperature
Going to bed now. Thank you for the replies sir.
ie site for a model, not Diviner!
In “A User’s Guide to the Moon” it says: “This increase in the mean temperature is related mostly to the temperature dependence of thermal conductivity of the topmost 1 to 2 cm of the soil”
A GHE of the soil? 🙂
Ah, “due to increasing contribution of radiative heat transfer between the particles at high temperatures”
http://faculty.washington.edu/sew2/ThermalToolkit/Tdep/index.html
Amazing that climate modelers have never created this basic model. Instead they start with a flat Earth model illuminated with a one quarter of a real insolation. Thank you, Dr. Spencer.
Well, modelers don’t do that, except as just a rough approximation for getting basic concepts across. Climate models are, in effect, run on a sphere. But, yeah, too many people think you can just use a global average absorbed flux to get a global average emitting temperature. But it will always lead to an over-estimate of the temperature when you do that.
Dr Spencer,
Just to clarify for me if you would (for I have not followed the entire debate over the past 2 posts), could you state whether or not you believe that the difference between the expected radiating temperature and observed surface temperature of the earth is mainly accounted for by the presence of greenhouse gases in the atmosphere?
Thank you.
TFN
Basically, yes, that’s what I believe. Convection mutes the surface warming of the greenhouse effect, but the net warming is due to the greenhouse effect. Convection. Wouldn’t even exist without the GHE.
Convection is triggered by large enough temperature gradients. Vertical gradients are established through greenhouse effect, yet even in the absence of GHG on a spherical earth meridional gradients are expected to appear and large scale motion of air as in the Hadley cell or general atmospheric circulation would also redistribute the heat vertically and horizontally. The day-night cycles are also expected to result in temperature gradients that induce convection and heat redistribution on more local scales.
As compared to your no-atmophere earth example in previous post shouldn’t this in principle even further reduce the 5 C difference you ended up in mean surface temperature because of the non linearity in SB law ?
Dr. Spencer,
Why do you assume that increased convection only mutes a portion of a radiative greenhouse effect, rather than the whole 33C? That convection dominates over radiative-convective equilibrium in the troposphere?
Calculations support that convection dominates ~92% of heat transport in the troposphere. Paper(s) available on request, but I won’t post a link now since comments with links on your site in my experience disappear, never to be seen again.
Best regards.
Um….because the surface temperature is STILL 33 deg. C warmer than without an atmosphere, right?
Maybe you are misinterpreting what the “33 deg C warming” number represents. It is the final result AFTER convective cooling has reduced the pure radiative greenhouse surface warming, which would be around 60 deg. C of warming (for an assumed albedo of 0.3, and constant RH). So, convective cooling negates about 60% or so of the greenhouse surface warming. So, yes, convective cooling is extremely strong…but it still leaves 33 deg. C (or so) of greenhouse warming left over.
“because the surface temperature is STILL 33 deg. C warmer than without an atmosphere, right?”
Yes, but that 33K “gravito-thermal greenhouse effect” or surface temperature “enhancement” due to atmospheric mass/gravity/pressure, not radiation. The Earth surface temperature (& that of 8 other planets) can be determined solely as a function of solar insolation and surface pressure (Nikolov & Zeller & many others), a gravito-thermal GHE, not radiative GHE.
The entire tropospheric temperature profile of the 1976 US Standard Atmosphere & Earth surface temperature can be accurately calculated by the “greenhouse equation” as a function of solar insolation and atmospheric pressures, and no greenhouse gas radiative forcing.
Spaces inserted in link – remove spaces:
hockeyschtick.blogspot. com /2014/12/why-us-standard-atmosphere-model.html
If you had 5 times the existing atmospheric pressure, and the air was radiatively inert, the surface temperature would be the same as if there was no atmosphere. But you go ahead and keep believing that silliness. Let me know when you have a time dependent model that creates observed temperatures from energy fluxes (which, btw, determine all temperatures) given any arbitrary initial temperature conditions.
“If you had 5 times the existing atmospheric pressure, and the air was radiatively inert, the surface temperature would be the same as if there was no atmosphere.”
That’s false. Please read Feynman’s Chapter 40 on statistical mechanics of the atmosphere where he proves a radiatively-insert column of the non-greenhouse gas N2 would indeed develop a temperature gradient in a gravitational field, due to the kinetic theory of gases/i.e. a Boltzmann distribution.
hockeyschtick.blogspot. com /2015/07/feynman-explains-how-gravitational.html
Secondly, the same kinetic theory of gases/ideal gas law can be used to accurately compute the surface temperature of Venus and without any GHG radiative forcing whatsoever (data from the NASA fact sheet).
T = PV/nR = 92000/(65000/43.45*0.083144621) = 739K
No radiative calculations are necessary to compute Venus temperatures to within 2K of observations. Thus, are you claiming that if the Venus pressures were 5X lower, there would be no change of the Venus surface temperatures? This is clearly not true.
Omg. You seriously don’t understand the ideal gas law. It does NOT explain why the temperature is what it is. It tells you how pressure, density, and temperature are related for a gas. For example, for the surface pressure on Venus, IF you knew the density, then you know the temperature. But the density DEPENDS ON the temperature. It’s circular reasoning.
“It tells you how pressure, density, and temperature are related for a gas.”
Of course, all of these variables are inter-related by the Ideal Gas Law, and for constant pressure, temperature and density are inversely related (that is, if there are fewer molecules in a given volume, they of course need to be travelling at a greater average speed to exert the same pressure). Of course, any change in any one variable will cause changes in the others via the IGL, but that is not circular reasoning. E.g. if the Venus pressure was reduced 5X, there would be a ~5X reduction in temperature via the IGL, not no change in temperature as you appear to suggest.
How is it possible, Dr. Spencer to very accurately calculate the surface temperature of 9 planets solely on the basis of solar insolation & surface pressure, and without any GHG radiative calculations whatsoever, using the Poisson Relation, which in turn is derived from the Ideal Gas Law? [Nikolov & Zeller & others]
hockeyschtick.blogspot. com /2014/03/why-ideal-gas-law-gravity-atmospheric.html
And how is it possible to derive the surface temperature and the tropospheric temp profile of the 1976 US Std Atmosphere using the gravito-thermal “greenhouse equation” without any GHG “radiative forcing” calculations whatsoever?:
hockeyschtick.blogspot. com /2014/12/why-us-standard-atmosphere-model.html
Did you read Feynman Ch 40 where he proves a column of pure N2 in a gravitational field would establish a Boltzmann distribution/temp gradient?
“How is it possible, Dr. Spencer to very accurately calculate the surface temperature of 9 planets solely on the basis of solar insolation & surface pressure”
If you simply tune your favorite model to fit to the data, you will certainly fit the data.
“T = PV/nR = 92000/(65000/43.45*0.083144621) = 739K”
For that to work you had to know Venus density(z) (ie. V/n)which was measured by NASA from radio signals. They then used the formula with only 1 unknown to compute T(z). Otherwise as Dr. Spencer implies you had 1 eqn., two unknowns.
“And how is it possible to derive the surface temperature and the tropospheric temp profile of the 1976 US Std Atmosphere using the gravito-thermal “greenhouse equation””
The Standard Atm. has all the radiative balance input already in there. Let’s see you derive planet global Tmedian surface temperature from just insolation and surface pressure. Without any curve fitting at all, without any temperature measurements at all or any density measurements.
Insolation TOA 1371 W/m^2
Surface pressure 1bar
You will find you can’t, you will need radiative balance techniques (LBLRTM) which work to within 1% of soundings on Earth and Venus for T(z).
Hockeyschtick: You ask, “Did you read Feynman Ch 40 where he proves a column of pure N2 in a gravitational field would establish a Boltzmann distribution/temp gradient?”
Why do you continue to slander Feynman? He asserts no such thing, and in fact, he asserts exactly the opposite, that there would be no vertical temperature gradient in an isolated column of gas in a gravitational field. He disposes of that issue in just a few sentences.
He goes on to demonstrate how there would be a vertical pressure gradient in such a system. You do understand the difference between pressure and temperature, don’t you? (I’m actually not sure you do!)
You completely misunderstand what the Boltzmann distribution is. It is the distribution of velocities of molecules at any location in equilibrium. It is NOT a function of height!
Your continued misinterpretations, misreadings, and misunderstandings mean that no one will take you seriously.
“If you simply tune your favorite model to fit to the data, you will certainly fit the data.”
There is no “tuning” or curve fitting whatsoever. The surface temp on the 9 planets is determined from only 2 variables: surface pressure and solar isolation, and NO fudge factors are needed for “tuning.” The equation determined exactly matched the Poisson Relation, which is derived from the Ideal Gas Law. In contrast, when Nikolov and Zeller models greenhouse gas partial pressures vs. surface temperature, the standard error was was 20 TIMES worse vs. the “gravito-thermal” model. If fact, it was not possible to “tune” the model based on GHG partial pressures, since the temperatures on the planets are NOT dependent on GHG concentrations.
T = PV/nR = 92000/(65000/43.45*0.083144621) = 739K
“For that to work you had to know Venus density(z) (ie. V/n)which was measured by NASA from radio signals. They then used the formula with only 1 unknown to compute T(z). Otherwise as Dr. Spencer implies you had 1 eqn., two unknowns.”
NASA measured the temperature, density, and pressure on Venus, and clearly those values are exactly as expected for the gravito-thermal GHE [defined by the IGL/Poisson Relation] on Venus, with NO room left over for any sort of radiative greenhouse effect, otherwise the Venus temperatures would be much, much higher.
And how is it possible to derive the surface temperature and the tropospheric temp profile of the 1976 US Std Atmosphere using the gravito-thermal greenhouse equation
“The Standard Atm. has all the radiative balance input already in there. ”
Clearly you don’t know what you’re talking about. There are ZERO radiative calculations in the US Standard Atm mathematical derivation. There is ZERO “radiative balance input in there.”
If you disagree, show the equation for radiative input to the US Std Atm. and if you read my post, you would understand how the Std Atm. is calculated from Newton’s Second Law of motion F = ma = mg, and the 1st Law of Thermo., neuther of which involve any “radiative forcing” calculations.
“Lets see you derive planet global Tmedian surface temperature from just insolation and surface pressure.”
Sure, all of the mathematics are here and in many other HS posts. I have derived not only the surface temperature, but the entire Std Atm. tropospheric temp profile from only solar insolation and surface pressure:
hockeyschtick.blogspot. com /2014/11/the-greenhouse-equation.html
HS says: “There is no “tuning” or curve fitting whatsoever.”
Bushwah. See page 17 N&Z: “Function (5) was fitted to each one of the 12 sets of logarithmic 𝜋𝑖 pairs generated by Equations (1) and (2) and shown in Table 4. Figures 1 and 2 display the resulting curves of individual regression models..”
Function (5) is a “four-parameter exponential-growth function”. You know what they could have done with 5 parameters.
Wow Ed Bo, so many misunderstandings in your single comment!
Ed Bo says, “Why do you continue to slander Feynman? He asserts no such thing, and in fact, he asserts exactly the opposite, that there would be no vertical temperature gradient in an isolated column of gas in a gravitational field. He disposes of that issue in just a few sentences.”
Baloney. Feynman walks through a thought experiment and begins with the assumption an N2 column would be isothermal. In the next step he clearly proves why it would not be isothermal in a gravity field. What part of “It is not an isothermal atmosphere” as Feynman explains for a N2 column & the atmosphere do you not understand? Thus, it is you who is effectively slandering Feynman with your misinterpretations.
“He goes on to demonstrate how there would be a vertical pressure gradient in such a system. You do understand the difference between pressure and temperature, dont you? (Im actually not sure you do!)”
Wow, clearly you are the one who doesn’t understand. The change in temperature and pressure with height is governed by the Poisson Relation, which is in turn derived from the Ideal Gas Law, and with ZERO input from GHG “radiative forcing.”
“You completely misunderstand what the Boltzmann distribution is. It is the distribution of velocities of molecules at any location in equilibrium. It is NOT a function of height!”
You obviously have no clue…Feynman in 40-2 specifically describes the non-isothermal atmosphere as a Boltzmann distribution which follows the Boltzmann Law. Heere’s how to calculate the Boltzmann distrbution on Earth, and the effect of an atmosphere without GHGs.
hockeyschtick.blogspot. com /2014/11/why-greenhouse-gases-dont-affect.html
The great physicist Maxwell also proved “In the convective equilibrium of [atmospheric] temperature, the absolute temperature is proportional to the pressure raised to the power (γ-1)/γ, or 0,29.” which is simply a re-statement of the Poisson Relation.
hockeyschtick.blogspot. com /2014/05/maxwell-established-that-gravity.html
“Your continued misinterpretations, misreadings, and misunderstandings mean that no one will take you seriously.”
Ditto to you.
HS says: “NASA measured the temperature, density, and pressure on Venus”
The Russians measured the temperature and the pressure in situ. NASA measured the density from refraction of orbiter radio signals and extrapolated the T(z) results to the surface.
HS writes: “those values are exactly as expected for the gravito-thermal GHE [defined by the IGL/Poisson Relation]”
Yes, of course they are, once Venus density(z) was known from refraction, NASA used IGL to compute T(z) and T(0). So of course the gravito-thermal works, that is what they used. IGL is universal HS. Works on Venus too. And even other planets. Even exoplanets!
Hs: “Clearly you dont know what youre talking about. There are ZERO radiative calculations in the US Standard Atm mathematical derivation.”
Clearly HS doesn’t know the US Standard Atm. was derived from a committee vote. Based on midlatitude tropics sounding rocket data, that had all the radiative balance nature provided.
HS: “Sure, all of the mathematics are here and in many other HS posts”
Nope, you used a measured temperature in that post and then a gradient. Thus you used radiative balance & way more info. than your claim to use only:
Insolation TOA 1371 W/m^2
Surface pressure 1bar
If not, show us right here. Just those two numbers ought to do it if you can, but you won’t be able.
Ball: The authors investigated 12 different models/regressions, most of which DO consider GHG partial pressures, but only one model of the 12 outperformed {by a factor of more than 20 TIMES less standard error} the other 11 modeled permutations and combinations. The one model that outperformed just so happens to exactly match the Poisson Relation formula. As the authors state, this cannot be by chance alone. The Poisson Relation equation is NOT a curve fitting exercise and is easily calculated as I have done in the posts above from the 1st Law of Thermo and Newton’s second Law of Motion F=ma=mg. That is why I stated There is no tuning or curve fitting whatsoever necessary to show that all of these planets fulfill the Poisson Relation and thus the gravito-thermal GHE, with surface temperatures accurately determined fron only TWO variables, pressure and solar insolation for all of the planets. If there was a true radiative GHE on ANY of these planets, the models which considered GHG partial pressures should have been far more accurate than the single one considering pressure instead; instead, the opposite is found.
Ball claims “Clearly HS doesnt know the US Standard Atm. was derived from a committee vote. Based on midlatitude tropics sounding rocket data, that had all the radiative balance nature provided.”
That’s false, and the entire mathematical derivation of the US Std Atm is in the document here. There was no “committee vote” on anything, and the mathematical derivation uses the same barometric formulae I used in deriving the gravito-thermal GHE equation, and not one signle radiative calculation, and which was confirmed by millions of rocket and radiosonde observations.
The greenhouse equation reproduces the US Std Atm essentially perfectly from the surface to top of the troposphere, and the only radiative forcing in that equation is solar insolation. There is no input for GHG radiative forcing whatsoever. The GHE and temperature profile is derived from solar insolation and atmospheric mass/gravity/pressure alone.
http://hockeyschtick.blogspot.com/2014/11/the-greenhouse-equation.html
HS: “The one model that outperformed just so happens to exactly match the Poisson Relation formula.”
The curve fit for that one (Model 12) is shown in eqn. (10a). That curve fit regression is not exactly the IGL; please cite the N&Z paper’s words not yours.
Remember HS, Feynman also said the easiest one to fool is yourself.
“you used a measured temperature in that post and then a gradient. Thus you used radiative balance & way more info. than your claim to use only:
Insolation TOA 1371 W/m^2
Surface pressure 1bar”
I did not “use a measured temperature” for either the equilibrium temperature with the Sun (which is CALCULATED using the Stefan-Boltzmann Law for SOLAR input only) or for the surface temperature of Earth, which is CALCULATED by the equation, NOT assumed.
I’ve given you links to the “greenhouse equation” several times. Name specifically one single ASSUMED temperature in that equation. You cannot.
HS: “Thats false..”
The easiest one to fool is yourself HS.
Don’t download this on a dial up 300 baud modem. Hypothetical atm. accepted by COESA, adopted, approved by ISO Members:
http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770009539.pdf
Ball: per your request from N&Z:
“The fact that only one
of the investigated twelve non-linear regressions yielded a tight relationship suggests that
Model 12 might be describing a macro-level thermodynamic property of planetary
atmospheres heretofore unbeknown to science. A function of such predictive skill [i.e. not curve-fitting] spanning
the breadth of the Solar System may not be just a result of chance. Indeed, complex natural
systems consisting of myriad interacting agents have been known to exhibit emergent
behaviors at higher levels of hierarchical organization that are amenable to accurate modeling
using top-down statistical approaches (e.g. Stolk et al. 2003).”
HS: “I did not use a measured temperature for either the equilibrium temperature with the Sun (which is CALCULATED using the Stefan-Boltzmann Law for SOLAR input only) or for the surface temperature of Earth, which is CALCULATED by the equation, NOT assumed.”
Ok, see! You used a temperature from radiative balance. If not, show us right here from just:
Insolation TOA 1371 W/m^2
Surface pressure 1bar
no temperature in that list, you have to derive the temperature from those data alone, IF you can back up your claim. You won’t be able since:
The easiest person to fool is yourself.
HS: “Ball: per your request from N&Z:”
When called out, HS backs down using N&Z own words, Model 12 not exactly the IGL after all.
The easiest one to fool is yourself HS.
Ball4: The mathematical derivation of the US Std Atmosphere 1-D model is almost 50 pages of barometric & physical chem calculations, not just a “committee vote” on the final product as you try to pass it off as. There is not one single radiative calculation in the 50 pages of derivations. In fact, the effect of CO2 was calculated as insignificant and their model therefore completely ignored CO2 in their physical chem & barometric calculations.
The exact same barometric formulae were used to derive the gravito-thermal “greenhouse equation,” which CALCULATES, not assumes, the equilibrium temperature with the Sun and the surface temperature and temperature profile of the troposphere.
Ball4 claims “When called out, HS backs down using N&Z own words, Model 12 not exactly the IGL after all. The easiest one to fool is yourself HS.”
Baloney. That’s great, misquote me to fabricate a false criticism. Model 12 is essentially the same as the Poisson Relation, NOT the IGL, even though the POISSON RELATION is DERIVED from the IGL as stated by me and N&Z:
“The functional response of Eq. (10a) portrayed in Fig. 4 closely resembles the shape of
the dry adiabatic temperature curve in Fig. 7a described by the Poisson formula and derived
from the First Law of Thermodynamics and the Ideal Gas Law (e.g. Wallace and Hobbs
2006, p. 78)“
HS: “their model therefore completely ignored CO2”
Correct. So you can not therefore use the Standard Atm. to argue there is no effect of CO2, since that is circular reasoning after they ignored the effect. They just used IGL and hydrostatic atm. which is good enough for their purposes such as aircraft altimeter calibration – close enough to keep them separated 1,000 feet vertically.
A very good lesson in learning the easiest one to fool is yourself.
I quoted you exactly HS, your words. Now after being called out about Model 12, you change wording to “is essentially the same” as IGL. Better to use N&Z words exactly as you clipped them HS.
The easiest to fool is yourself HS.
“Correct. So you can not therefore use the Standard Atm. to argue there is no effect of CO2, since that is circular reasoning after they ignored the effect. They just used IGL and hydrostatic atm. which is good enough for their purposes such as aircraft altimeter calibration close enough to keep them separated 1,000 feet vertically.
A very good lesson in learning the easiest one to fool is yourself.”
You need to look in the mirror yourself, Ball4, since I’ve already pointed out many of your multiple false and strawman arguments, repeatedly. I just told you they did calculate the effect of CO2, determined it to be insignificant, and therefore dropped it and other trace gases from the model. There is nothing circular about calculating the effect of CO2 to be negligible! It simply goes to prove CO2 has no measurable effect upon temperatures. The entire 33C gravito-thermal GHE and the even larger negative 35C anti-greenhouse effect from the center of mass at ~5.2km to top of the ~220K troposphere is easily explained by the gravito-thermal GHE and calculated by the same barometric formulae in the HS “greenhouse equation.” If there was also a 33C radiative GHE in addition, the Earth surface temp would obviously be much, much higher than it is.
Ball4 says “Now after being called out about Model 12, you change wording to is essentially the same as IGL. Better to use N&Z words exactly as you clipped them HS. The easiest to fool is yourself HS.”
Ball4 has fooled himself yet again by claiming he “called me out about Model 12” when in fact he has not called me out on anything at all, and obviously doesn’t understand the difference (or derivation) of the Poisson Relation from the IGL.
The easiest to fool is yourself Ball4.
I used no straw men HS, I quoted N&Z exactly, I quoted you exactly and I showed where the Stnd. Atm. comes from, exactly.
Oh and by the way “from the center of mass at ~5.2km”, the center of mass of Earth atm. is not 5.2km, the COM is way above that. I’ll show how to calculate our atm. COM correctly if you can back up your 3:06pm claim “The Earth surface temperature…can be determined solely as a function of solar insolation and surface pressure” meaning exactly – without radiative balance, curve fitting and/or density(z).
Insolation TOA 1371 W/m^2
Surface pressure 1bar
Ball4 You are again absolutely incorrect again in claiming the center of MASS is “way above” 5.2km. The atmospheric pressure at the center of mass is where the atmospheric pressure is 0.5 atmospheres, which by US Std Atm. is at ~5.1-5.2km, just as I stated.
hockeyschtick.blogspot. com /2015/09/why-effective-radiating-level-erl-is.html
I’ve shown all my work at these links, so now it’s time to show your (nonexistent) math Ball4, if you have any.
I’ve have shown over and over that the greenhouse equation calculates surface temp and tropo temp profile without using ANY assumed temperature or GHG radiative forcing. Sorry you seem incapable of understanding the concepts involved and I’m done trying to explain them to you repeatedly and with the multiple links you obviously haven’t read or understood. It’s easy to fool yourself Ball4 when you fabricate strawmen and false claims.
N&Z: “3.1.3. Similarity of Model 12 to Poissons Formula”
Poisson formula HS, and “similarity”, “resembles” not “essentially same as”.
I see HS can not back up his claim, referring us elsewhere won’t work with this crowd. Plus I don’t see HS refer to any experiments such as Dr. Spencer has done and from which HS could benefit.
“N&Z: 3.1.3. Similarity of Model 12 to Poissons Formula
Poisson formula HS, and similarity, resembles not essentially same as.”
Yet another Ball4 strawman/false argument. Figure 7 shows the Poisson Relation curve vs. the Model 12 regression curve and they are indeed similar and essentially the same formulas & curves, as I have repeatedly pointed out.
“I see HS can not back up his claim, referring us elsewhere wont work with this crowd.”
I have referred you to my own posts with all of the underlying math to back up ALL of my claims and which is too lengthy and unnecessary to repost here. You, on the other hand, have no mathematical basis for any of your strawman/false claims. THAT is what truly “won’t work with this crowd.”
HS: “which is too lengthy and unnecessary to repost here.”
Of course, again as I wrote, since that link falsifies your claim here HS, because that link shows you used a temperature from radiative balance and a gradient which is way more than your claim here of only using this to get planet surface temperature:
Insolation TOA 1371 W/m^2
Surface pressure 1bar
You could of course also use IGL with density(z) as NASA did because the planet radiative balance(z) is inherent in the measured density(z) but that was not your claim.
The center of gravity of the atm. trivial answer is center of earth. However, if one starts from the surface on a per unit area basis the PE of the column from surface to infinity is the cg * Ma * g. If the column is heated by the sun, the PE increases as cg rises (Ma total mass). Dunno what happens to the height where “atmospheric pressure is 0.5 atmospheres” so in that case perhaps HS can show us PE increases from that by the same amount.
Roy Spencer says, September 29, 2016 at 3:23 PM:
True. But the bulk atmosphere would be much warmer in the steady state than it is now. Not because of its larger mass, but because it’s radiatively inert.
Roy Spencer says, September 29, 2016 at 5:13 PM:
Very true.
HS says: “Please read Feynmans Chapter 40 on statistical mechanics of the atmosphere where he proves a radiatively-insert column of the non-greenhouse gas N2 would indeed develop a temperature gradient in a gravitational field, due to the kinetic theory of gases/i.e. a Boltzmann distribution.
hockeyschtick.blogspot. com /2015/07/feynman-explains-how-gravitational.html
Thanks for my chuckle of the morning!
Feynmann EXPLICITLY states (twice in the first paragraph you quote!) that the equilibrium atmosphere will be isothermal
“If the temperature is the same at all heights …”
“… since the temperature is constant in this problem.”
Then he goes on to explain why earth’s atmosphere should not be expected to be isothermal (and also why heavier gases don’t tend to settle out toward the bottom)… because it is not in equilibrium!
“This does not really happen in our own atmosphere, at least at reasonable heights, because there is so much agitation which mixes the gases back together again. It is not an isothermal atmosphere.”
In other words, HS completely mis-interprets Feynmann!
HS: You say, “Feynman walks through a thought experiment and begins with the assumption an N2 column would be isothermal.”
No he doesn’t! He PROVES through the most basic thermodynamic analysis why such a column MUST be isothermal in equilibrium, and after stating that our own atmosphere is NOT.
What can we conclude from this, using the most basic logic skills? First, that our atmosphere is not thermodynamically isolated, and second, that the reasons for its lapse rate come from the fact that it is not thermodynamically isolated.
Ball4: “Of course, again as I wrote, since that link falsifies your claim here HS, because that link shows you used a temperature from radiative balance and a gradient which is way more than your claim here of only using this to get planet surface temperature”
Wrong again. What link are you referring to, as none of the links falsify my statements. No matter how many times it has been explained to you, NO temperature is assumed by the gravito-thermal GHE equation. Here’s the equation once again, proving there is absolutely no assumed temperature T on the right side of the equation. The only inputs are surface pressure (P, 1 atm), albedo (a), gravity (g), mass (m), & the solar constant (S). That’s it, NO temperatures on the right side of the equation.
http://3.bp.blogspot.com/-xXJOurldG_E/VHjjbD6XinI/AAAAAAAAGx8/8yXlYh8Lcr4/s1600/The%2BGreenhouse%2BEquation%2B-%2BSymbolic%2Bsolution%2BP.png
hockeyschtick.blogspot. com /2014/11/the-greenhouse-equation-predicts.html
The “Greenhouse Equation” calculates temperature (T) at any location from the surface to the top of the troposphere as a function of atmospheric mass/gravity/pressure and radiative forcing from the Sun only, and without any radiative forcing from greenhouse gases. Note the pressure (P) divided by 2 in the greenhouse equation is the pressure at the center of mass of the atmosphere (after density correction), where the temperature and height are equal to the equilibrium temperature with the Sun and ERL respectively.
Hockey Schtick says:
“Why do you assume that increased convection only mutes a portion of a radiative greenhouse effect, rather than the whole 33C? That convection dominates over radiative-convective equilibrium in the troposphere?”
Actually, you have pretty much answered your own question when you talked about there being a temperature gradient (i.e., lapse rate) in the atmosphere. You wrongly attribute this to some magical pressure effect but the reason for the gradient is simple to explain: Convection is ineffective in completely eliminating the greenhouse effect because in order to do so, convection would have to drive the atmosphere to an isothermal state; then the greenhouse effect would be eliminated. However, the atmosphere is only unstable to convection when the lapse rate is steeper than the (appropriate dry or moist) adiabatic lapse rate. So, convection cannot drive the atmosphere to such an isothermal state…It can only drive the lapse rate down to the adiabatic lapse rate.
In fact, your buddies Nikolov and Zeller illustrated part of this fact themselves: They wrote a silly “paper” that Tallbloke and Anthony Watts picked up (although Anthony later distanced himself from it after Willis Eschenbach convinced him it was garbage). In that paper, they claimed to demonstrate that convection, when added to a simple radiative shell model in what they claimed was a more correct manner, causes the greenhouse effect to disappear. However, what they actually did was add convection to the model in an INCORRECT manner because (by their own description!) they added it in a way that drove the atmosphere to an isothermal state (i.e., the shell to the same temperature as the surface). The fact that the lapse rate is necessary for the greenhouse effect to operate is something that is well-known (e.g., discussed in Ray Pierrehumbert’s book).
As for your claim that the ideal gas law somehow constrains the temperature: It does not. It is easy to demonstrate that the hydrostatic condition plus the ideal gas law are compatible with any temperature distribution that you so desire. Changing the temperature distribution just changes the way the density (and pressure) decrease with height. The decay is exponential if the temperature distribution is isothermal but deviates from that if the temperature distribution is something else.
HS 2:02pm: “The only inputs are surface pressure (P, 1 atm), albedo (a), gravity (g), mass (m), & the solar constant (S).”
No HS, you used a measured equilibrium T(z) input also as I wrote up-thread. But HS does now tacitly admit being wrong starting this sub-thread in writing “The Earth surface temperature..can be determined solely as a function of solar insolation and surface pressure”.
Here HS admits more inputs are really necessary into a purported equation for planet surface global Tmedian. Among these inputs HS self cites an eqn. developed from knowing the equilibrium T(~5.2km) = 255K (~5.2km effective emission level) from measurements. Which is what I noted above knowing any T(z) measured or from energy balance will always be needed along with gradient.
If, for example, CO2 added ppm moves the equilibrium 255K up to 5.3km, then this equation will change with the new P at the higher atm. effective emission level forced by the sun since Earth atm. composition matters as proper measurements or energy balances determine.
As I said, The only inputs [to the greenhouse equation] are surface pressure (P, 1 atm), albedo (a), gravity (g), mass (m), & the solar constant (S).
No Ball4, the equation absolutely does CALCULATE the 255K equilibrium temperature with the Sun, and does not use any “measured” equilibrium temperature as you claim.
First of all, the equilibrium temperature of Earth with the Sun isn’t an observation as you claim, it is CALCULATED using the solar constant and albedo, both of which are constants, via the Stefan-Boltzmann Law. I have used in the greenhouse equation the exact same mathematics in countless textbooks for calculating the equilibrium temp with the Sun of 255K.
In the greenhouse equation, S, P, g, m, heat capacity at constant pressure (C), albedo (a) are all CONSTANTS, not variables, and the only variables are the tropospheric height s for which the equation calculates the average temperature, perfectly reproducing the 1976 US Std Atmosphere at intervals of every 200 meters throughout the ~10km troposphere.
hockeyschtick.blogspot.com/2014/12/why-atmospheric-temperature-is-linear.html
Therefore, I was correct to state The Earth surface temperature..can be determined solely as a function of solar insolation and surface pressure, because all of the other variables are CONSTANTS for Earth’s atmosphere.
HS points out the obvious: “I have used in the greenhouse equation the exact same mathematics in countless textbooks for calculating the equilibrium temp with the Sun of 255K.”
Ok, see! Again, calculated the measured 255K at the measured 5.2km altitude of the Standard Atm. You had to use a T(z) at a z which falsifies your claim of only using constants.
“Therefore, I was correct to state The Earth surface temperature..can be determined solely as a function of solar insolation and surface pressure”
No, you used an energy balance also; the calculated, measured 255K. All you need to get your results is any T(z) (measured or properly calculated by energy balance) and a gradient as I have said all along. The T(z) CAN NOT be calculated solely from solar insolation and surface pressure as you claim. That is just plain false.
And, I know this may be hard on you HS, getting it wrong so often, but your eqn. adds and apparently subtracts temperatures which isn’t physical. I can’t pour a glass of water at 72F into another 72F water and add them to 144F as you have done. Your eqn. does that very obviously. False physics HS. Try to learn the energy balance you found in all those texts, there you are on to something good, correct atm. radiation physics. Extend that learning to LBLRTM and you will be back on the reservation.
No Ball4, you’re wrong about the greenhouse equation once again.
For the final time, the one and only temperature in the greenhouse equation is the T(h) on the LEFT side of the equation, and NONE of the variables or constants on the RIGHT side are temperatures. This same equation calculates the To at the surface, the Te at the center of mass, and the tropospheric T at ANY height (h) in the troposphere. Your claim that an assumed temperature is hiding somewhere on the right side of that equation that is absolutely false.
Once again, the surface temperature and the temperatures at every single geopotential height (h) in the troposphere are calculated by only changing the geopotential height (h) as every other “variable” of the equation is a constant for Earth.
My claim? No, it is HS claim:
“Note the pressure (P) divided by 2 in the greenhouse equation is the pressure at the center of mass of the atmosphere (after density correction), where the temperature and height are equal to the equilibrium temperature with the Sun and ERL respectively.”
“local horizontal equilibrium at that particular height must by definition bewhere T = equilibrium temperature with the Sun = 255K”
And sure enough your line goes right thru your calculated (& measured) 255K by eqn. design. And of course, once again, your equation adds temperatures, which is the most obvious incompetent physics problem.
Want to circle back again HS? I’ll just write the same observations.
HS, what you have done here in a round about way is to simply find a line that satisfies y=mx+b. m being the slope (you know DALR -g/Cp or Stndrd. 6.5) then use one temperature for when y=5.2km, x=0, the observed/calculated 255K and you have b & the line eqn. Now you can compute any other x at any y. This works as it is the line showing neutral stability in the temperature field of the trop. which is what the Standard atm. table does. Not what the T actually is, only hypothetical neutral buoyancy line. Parcel with T above this line are too high, they move down by losing energy to surroundings. And vice versa. This has been known for a very long time.
With added CO2 ppm, or other IR active gas, the m won’t change much at all, but the intercept b will change. You can only get new b from the new energy balance. You have made this harder than I have ever seen but, hey, it looks like a cool eqn.
As for how N&Z have done what they have done: I haven’t looked in detail at the latest incarnation of their work but I assume it is similar to the original which was just a curve-fitting exercise, although there was also some suggestion that the fitting procedure might have gone both ways. I.e., the data was not known that accurately for some of the bodies and they may have decided on the values they chose with the help of their fitting equation rather than the other way around. Whether they did this or not, I do not know but I do know that it often doesn’t take many free parameters to fit data when you are free to choose also the functional form,etc…Hence the statement attributed to von Neumann that “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.”
It fascinates me that with all the bone-headed mistakes that they made (and never acknowledged as far as I know) such as putting in convection incorrectly into the shell model, Nikolov and Zeller are taken seriously by anyone. No wonder that they have to adopt pseudonyms (https://www.washingtonpost.com/news/morning-mix/wp/2016/09/19/scientists-published-climate-research-under-fake-names-then-they-were-caught/)
Thank you, Dr. Roy. In these last 2 posts, you have adressed a couple of issues that I have felt the need to calculate more than once, but didn’t find time for.
Hi Dr.Spencer,
I just read your interesting debate with Geoff above.
I would just highlight a strange behavior of the “Soil Temperatures on the Moon” simulator.
Selecting the “Depths” tab, it reports the inner layers starting temperature as a direct function of albedo, and it is not clear at which final temperature the model stabilize its result for the deepest layers.
Anyways, shouldn’t it be as an inverse function of albedo, not a direct one?
Have a great day.
Massimo
Geoff, I know Jack Schmitt, the astronaut who installed the subsurface temperature monitoring equipment on Apollo 17. I’ll ask him about the warm subsurface. From what I’ve read this morning, it sounds like the subsurface is kept warm by radioactive decay, and the very low thermal conductivity of the surface layer insulates the deeper layer, maintaining a large temperature gradient.
Prof Humlum @ Climate4you global temperatures has empirical data showing that periods with relatively high planetary rotation velocity (and low LOD) tend to be associated with relatively warm periods, and vice versa .
http://www.climate4you.com/
Dr Spencer,
You wrote ”
“. . . the pure radiative greenhouse surface warming, which would be around 60 deg. C of warming (for an assumed albedo of 0.3, and constant RH). . . ”
I presume this [now] 60 C of warming has been reflected in the [new] falsifiable GHE hypothesis.
It seems that the hypothesis now has to factor in speed of rotation as part of the effect. It’s all looking less and less like anything to do with a greenhouse.
Even rotation might seem to be a bit of a misnomer. The Poles have exactly the same rotational period as any other parts of the surface, but have long periods of continuous exposure to the Sun, alternating with equally long periods where the Sun barely rises above the horizon.
Averages may not be particularly useful –
“Although in the summer the temperature can reach 50 degrees Celsius in the shade and in the winter can reach -9 (minus nine), the average year round temperature is about 30 degrees Celsius. Between the 27th of December and the 18th of January some area of the Sahara becomes covered with a thin white layer very similar to frost in Europe, which turns the surface white and hence the name: “The White Nights”.”
If the average is around 30 C, what difference does it make? My location has an average of around 27 C, but the average mean min. does not drop below 23 C.
From the Diviner site –
“With the exception of Mercury, the Moon has the most extreme surface thermal environment of any planetary body in the solar system. At the lunar equator, mean surface temperatures reach almost 400K (260.6 F) at noon and then drop to below 100K (-279.4 F) during the night. For comparison, the mean surface temperature on Earth is a temperate 295K (71.6 F).
The Earth and Moon each receive the same flux of solar radiation; the important difference is that the Moon doesn’t have an atmosphere to insulate its surface.”
It seems the Diviner people agree with me – the insulating effect of the atmosphere reduces the amount of insolation, resulting in lower max and higher min temperatures on Earth.
The GHE desperately needs a falsifiable hypothesis to refute the Diviner team. As they point out, insulation keeps the extremes on Earth more equable than the Moon. Lower, not higher, daytime temperatures. Higher, not lower, nighttime temperatures!
Modelling and asserting notwithstanding.
Cheers.
I would have also thought a planet such as the earth, composed mainly of high heat capacity oceans would have a much higher surface temperature compared to a similar rotating silicate planet?
Does a planet with oceans have a higher surface temperature than a planet without oceans, all other things remaining the same?
I also am interested in the answer. When the sea level rose after the last glacial, the Earth got more ocean surface. So the Earth received more possibilities to store daytime solar energy which should result in [average] temperature rise. In the same time the Earth lost land surface – and land surface loses it’s energy quickly during night and winter. I wandered whether this could be one of the reasons for the rapid temperature rises at the end of a glacial – and the more gradual going down after the optimum.
I entered the volumetric heat capacity of granite into Dr Spencer’s spread sheet from the previous post. The volumetric heat capacity of granite is not quite half that of water. With granite the diurnal temperature range was almost double, while the global average temperature dropped about 4 deg K.
Feynman –
Speaking theoretically –
“So, ultimately, of course, the temperature becomes the same at all heights in a gravitational field.”
He goes on to point out, however, reality –
“It is not an isothermal atmosphere.”
Cannot be isothermal, if it is hotter at one end than the other!
No gravito-thermal effect, either. If static pressure created heat, the depths of the oceans would be very hot indeed! High pressure, filled, CO2 cylinders would be hotter than empty ones (after settling to surrounding temperature, of course).
Spinning an object does not somehow “fling off” heat. Slowing it down does not increase the speed at which its energy content increases, either. The Moon spins slowly. Still gets hotter and colder than the Earth.
Overall, has cooled faster – greater surface to volume ratio.
Cheers.
Mike Flynn says, September 30, 2016 at 12:18 AM:
And it (the troposphere) is warmer at one end than the other because heat is constantly moving into it, through it, and out of it. That’s how it works with a fluid subjected to gravity and heated from below. It’s called (natural) “convection”.
No heating at the bottom, and no cooling from the top, no net energy (“heat”) flowing through the fluid in question (with/inside the bulk mass of the fluid), in the steady state. And, consequently, no negative temperature gradient from the bottom up.
Not sure what point you are making.
Convection does not necessarily result from “hotter at the bottom”. Often in the tropics, as elsewhere, there is no convection, but the air at the bottom is very much hotter than the air above. Dead calm, stinking hot, no vertical or horizontal air motion.
An extreme example is the solar pond, where the bottom water may reach 90 C, many tens of degrees hotter than the surface, but no convection takes place. If it did, the pond would be of no use whatsoever.
Whether a body is subject to gravity or not, makes no difference to energy transfer, per se.
An iron rod, heated white hot at one end, doesn’t care whether you hold it up, down, or sideways.
Heat does not “flow” into and out of matter. This is the “caloric” theory, which was thrown out with things like the luminiferous ether, more than a century ago. Things have moved along since then. I’m pretty sure Feynman had it about right.
Cheers.
Mike Flynn,
Your solar pond is not a good case as these depend on a bottom layer of super saturated brine which inhibits convection. This hardly represents atmospheric conditions.
I think where you encounter a buoyant mass of air at the surface, you will see convection. Buoyancy is in respect to atmospheric conditions overhead, naturally.
mpainter,
The brine pond is just an example. It actually exists – I prefer things that exist, rather than thought bubbles.
The atmosphere is a fluid, albeit much less dense than water. Its fluid dynamics follow the same rules, I think.
People associate warmth with buoyancy. I’m just pointing out that this is not necessarily true.
I may sound a little picky, but if there are billions of dollars involved, who wouldn’t want everything to be correct – or at least well defined, so we all agree on the subject matter?
Cheers.
“The atmosphere is a fluid, albeit much less dense than water. Its fluid dynamics follow the same rules, I think. ”
Sand and smoke can be fluid.
The atmosphere is a gas. All gases, all liquids, and of course sand, are fluid, but difference of gases and liquids
is that a gas is compressible.
So water at bottom of ocean is roughly the same density as
water at the surface of the ocean, one difference is the gas in the sea water will be more compressed when at the bottom of the ocean.
Gases such as N2 and O2 can’t be normally turned into liquid
from pressure alone- need pressure and be at their critical temperature.
http://www.engineeringtoolbox.com/gas-critical-temperature-pressure-d_161.html
4000 meter under the oceans, one has 400 times 1 atm of pressure [14.7 psi]: 5880 psi, both N2 and O2 at that depth are still a gas. Whereas say CO2 could be liquid.
Or there have been discovered, lakes of CO2 at depth in the ocean- “On Earth’s surface carbon dioxide (CO2) is normally a gas, but in the cold, high-pressure ocean depths it cools and becomes a liquid. ”
http://news.nationalgeographic.com/news/2006/08/060830-carbon-lakes.html
So, not going to find lakes of N2 and O2 at bottom of the sea- because it’s warmer down there than their critical temperature.
So at bottom of atmosphere, the gases are compressed.
The average velocity of gases are the roughly the same
throughout the troposphere. And because gases are compressed at the surface [more dense] and going the same average velocity a cubic meter [or cubic cm] has more kinetic energy than a cubic meter at higher elevation [and less compressed]. If total kinetic energy in volume space is higher, then air temperature is warmer.
If you have some air at sea level which is say 20 C, and you heat the air, the air expands [or is less dense if warmer], but air is also colliding with each other and “averaging the velocity”. What moves is the effects of the collisions and/or the effect collision cause a body of air to rise. Or one can have convection without air movement- rather the effects of the collisions move and it’s likely
or probable that such effects of collisions if higher velocities, go upwards. And if have enough effects of collision going upwards, this can cause air masses to move upwards [thermals].
Mike Flynn says, September 30, 2016 at 7:11 AM:
The same point as Feynman is making. That if there were no continuous throughput of heat in the atmosphere, it would’ve ended up naturally isothermal from top to bottom, IOW, that an atmospheric temperature gradient is intrinsically connected to the fact that heat always moves into it, through it, and out of it, making it unable to reach thermodynamic equilibrium.
Did I say that convection MUST occur whenever it is “hotter at the bottom”? No.
Well, there sure cannot be any “natural convection” going on in a fluid if that fluid isn’t somehow in a gravity field.
That’s exactly what it does. It “flows” whenever there’s a temperature difference between two systems or regions. “Heat” in thermodynamics is simply defined as the energy in transit between two ‘places’ simply as a result of the temperature difference between those two places …
Kristian,
I merely made a statement that convection is not necessarily related to temperature difference. Another instance of correlation being taken as causation.
Convection, natural or not, is merely the movement of matter in a fluid. No gravity is required for matter to be either heated or cooled. In the sense that you use convection, I agree with you, but convection is not necessary for heating or cooling a fluid. It can be done quite easily in zero gravity. Watching a gas flame in zero gravity is interesting.
As to “heat”, there are many definitions. Here is one –
“In physics, heat is energy that spontaneously passes between a system and its surroundings in some way other than through work or the transfer of matter. When a suitable physical pathway exists, heat flows spontaneously from a hotter to a colder body.”
Not terribly rigorous, wouldn’t you agree?
Here are a couple more –
“a. A form of energy associated with the motion of atoms or molecules and capable of being transmitted through solid and fluid media by conduction, through fluid media by convection, and through empty space by radiation.
b. The transfer of energy from one body to another as a result of a difference in temperature or a change in phase.”
What definition do you claim is correct?
Heat seems to me to be a manifestation of quantum processes, and merely a term of practical convenience. “Heat flow” is a useful practical everyday description – something akin to “temperature” – useful but non-existent in physical terms.
I’ll go away for now. No offence intended, but climatologists tend to avoid definitions understood by real scientists, and instead redefine things as they go along.
Forcings, feedback, back radiation, greenhouse effect, climate, climate sensitivity, chaos – the list goes on. This is science?
Cheers.
Mike Flynn says, September 30, 2016 at 5:51 PM:
Isn’t it? I thought all heat transfers were …
Yes, as a result of a temperature difference. Or, really, the result of a pressure/density difference. Which is, however, also naturally associated with a temperature difference within the fluid (gas or liquid) in question.
Again, no one claimed it was. Gravity, however, IS required for natural convection to work.
Convection doesn’t “heat” or “cool” the fluid. It moves the internal energy around, within the fluid. From the heating end to the cooling end.
It’s as rigorous as you could ever get it. Read the passage again. It is simply the energy transferred from a hotter place to a colder place. No more, no less.
b. is exactly the same as your first definition above, only worded a bit differently. a. isn’t a thermodynamic definition of “heat” at all. It probably rather derives from some field of engineering.
I don’t claim anything. I point out. And what I point out is that “heat” [Q] in standard, modern thermodynamics is defined as your b. above: “The transfer of energy from one body to another as a result of a difference in temperature (or a change in phase).”
This I kind of agree with. But once you understand the thermodynamic concept of “heat” [Q], talking about a “flow” of heat does make sense, even though it’s probably not terribly accurate in a strictly physical sense.
It’s obvious when you think about it. The solar side will eventually warm to the same temperature whatever the rotation speed. The opposite side will have less time to cool on a faster spinning planet and will be warmer.
The rotational speed will mean that the faster spinning planet will retain more heat for the next day. (part of the greenhouse effect?)
Dear Dr Spencer, a nice observation. Doesn’t it help to solve or soften the Faint Young Sun Paradox? Or did the people discussing the paradox have taken this effect into account? When the Earth was newborn, its spinning must have been at least 10 or so percent faster, right?
I believe that a newborn earth is thought to have been a gas giant, cum Jupiter or Saturn. How might this circumstance affect matters, I wonder?
The dominant scientific view now is that the early solar system acted as a giant distillation column, with significant separation of the elements by weight.
The heavier elements largely stayed closer to the sun and coalesced into the inner “rocky” planets.
The lighter elements largely ended up farther from the sun and coalesced into the “gas giants”.
Does when Earth was born include a large body hitting Earth and then the subsequent formation the Moon?
If so is earth’s birth when Earth was proto-earth or is Earth’s birth counted as after this massive impact and subsequent cooling from a global lava ocean and the cooling or formation of rock allowing dating of the rock?
Or about 4.5 billion years ago or do you mean early than this?
Dr Spencer’s post concerns time, the time that a place on the planet has to warm in the sun before it cools in the night. It is important in determining the average temperature.
There is another important matter of time in determining the average temperature: the vicious rhetorical trick played by the catastrophic anthropogenic global (CAGW) warming people. A trick we should not let them get away with. They talk of “amplification” due to “positive feedback”. Talk of positive feedback has mighty powerful rhetorical and emotional impact, misleading as used by the CAGW people.
They make their story seem scientific by citing Bode’s book on electronic amplifiers. Their story is not about amplification in the proper and ordinary sense of the word that Bode uses. Amplification ordinarily means power gain, the added power being supplied by active circuit components (i.e. components that have arbitrary access to external power sources) The CAGW people are not actually referring to power gain. They are referring merely to accumulation of signal energy by delay of its exit, in a passive system with no access to external power sources. It’s not ordinary positive feedback; rather it is reduction in negative feedback, through delay.
The increase in temperature is due to delay of exit of input signal power. The time that the input signal energy stays in the system is increased.
Mathematically, the Bode theory suitable is specially suitable for true amplifiers. It is built around the presence of a power-gain circuit element, connected in a feedback loop. The notion of loop gain is appropriate and helpful for that theory. Positive feedback refers to the loop.
For passive circuits, such as the climate system, that Bode mathematics is unsuitable. It is a misleading rhetorical artifice to shoehorn the climate system into that mathematics by pretending that passive Planck radiation is an active power gain element. This provides a pseudo-excuse for misleading emotive talk of “positive feedback”. In contrast, the natural linearized mathematics for passive systems is in terms of a straightforward transfer matrix, which is characterized by its eigenvalues, which do not refer to a loop. In a passive circuit, all eigenvalues are negative. There is no positive feedback in this sense.
This comment was stimulated by the importance of time in setting temperature. The CAGW people are tricksters. We should call them on this trick.
Christopher: I agree on your basic point that in climate science the term “positive feedback”, at least as describing the net effect, is used differently than it is apparently used in the engineering literature.
Basically, in climate science, they tend to think of the Planck response as the zeroth order effect rather than as a negative feedback. So, they calculate the no-feedback response (of ~1.2 K per CO2 doubling or 0.75 K per W/m^2) as being that which takes the Planck response into account and then they talk of a net positive feedback making the response larger.
Another way they could have done it (more in line with the engineering literature apparently) is to call the Planck response a negative feedback in which case what the temperature rises of 1.5 to 4.5 K per CO2 doubling that the IPCC is talking about still correspond to a net negative feedback, but a negative feedback smaller in magnitude than the Planck feedback.
I disagree with you, however, that there is any trickery involved. It is just another way of arriving at the same physical result. Whether you consider no response or the Planck response to be your “base case” is simply a matter of convenience. It is not surprising that in different fields, they arrive at different conventions.
In fact, Isaac Held argues that it might be more natural to consider the base case to be the one where relative humidity remains constant as temperature rises, which would then put the no-feedback response even higher and one would consider deviations from that to be net positive or negative feedbacks.
The fact that a certain convention gets scientists called “tricksters” is an indication more of the politically-charged environment surrounding the science where everything is suspect by those who don’t like the implications of the science.
“… but a negative feedback smaller in magnitude than the Planck feedback.”
I love this insight, Joel. I now have a new way to describe the processes and the feedbacks.
I agree that the use of “positive feedback” in climate science is not the same as the traditional use of “positive feedback” in electronics. I had just never thought of it as “less negative.” And often “less negative” is equivalent to “more positive, so the terminology makes sense in that context. (This also plays into the whole “warming” vs “less cooling” debate.)
Christopher, you are a very smart guy. 1) Read what I wrote about the planetary rotation rate having a large impact on average temperature. It’s very simple, it is a necessary consequence of the nonlinearity of the S-B equation combined with non-zero heat capacity of the surface.
2) bodes law is not contained in any climate model I’m aware of, whether the simple 1D models I run or the full 3D models. If there are issues analogizing climate feedbacks to electrical circuit feedbacks, they don’t affect climate model warming rates.
Dr Spencer, I am not quite sure to make of your comment here. You say that I am a smart guy. That alerts me, because, sad to say, I know I am very often mistaken. I am guessing your comment is a polite way of saying I am off-beam here.
My comment is based on my agreement with your post. I think that what you write about the planetary rotation is valid and about real physics, and, so far as I know, a new and interesting consideration in planetary science, hereafter perhaps to be known in the textbooks as ‘the Spencer effect’.
I agree with your immediately above comment except that I am not very smart, sad to say.
My comment was triggered by the part that time plays in your effect.
For the sake of clarity, I ought to have put in my post that I readily accept that there are important secondary effects of added atmospheric carbon dioxide, for example increased atmospheric water vapour and changes in clouds, taking the effect on optical thickness as primary. Such is real and valid physics.
But there are some points to make about the CAGW story of “positive feedback”, which is a popular way of referring to those secondary effects.
My main point is that it is emotionally powerful rhetoric that should be recognized as such. It is not the natural mathematical approach to the matter.
The loop gain of the positive feedback is less than 1, and therefore represents only a time delay, not an amplification. That time factor is the reason for my comment. I am using the word amplification in the sense of power gain as it is used by Bode. There is no power gain in the secondary effects of added carbon dioxide. They are therefore not amplification in Bode’s sense, though Bode is cited. I accept that the secondary effect, of added water vapour, contributes an addition to the temperature and to the energy content of the planet. But positive feedback with loop gain less than 1 cannot lead to runaway amplification in the way that positive feedback with loop gain greater than 1 does. Talk of “positive feedback” hints at the latter in a rhetorically emotionally effective way, and in that respect is misleading. I object to that. Bode’s theory is about active devices with arbitrary access to external power sources, not about passive systems such as the planetary energy flow. It is only by artifice and shoehorning that the CAGW people fit the latter into the Bode theory. I think that is objectionable.
The secondary effect, the delay of energy passage, is physically real. It is a valid secondary effect that makes an enhancing contribution to the temperature rise. It is an effect of time, not of power gain. I think it misleading to call it positive feedback.
This is a comment about rhetoric, not physics as such. As you say, the climate models don’t work as electronic circuits. The positive feedback and amplification story is merely a rhetorical popularization and simplification, not a description of the models. It is the models that are the real worry. There is reason to believe that the models are inaccurate, as you and others have shown. That reason is not connected with my complaint about the rhetoric.
This unfortunately is not a rhetorical issue.
The theory of the greenhouse effect is based on the concept of radiative forcing. An addition GHG would correspond to a forcing and is therefore regarded as an external source of energy. The confusion between energy and resistance (or time) therefore appears before the question of feedback. This confusion is the result of a thermodynamically untenable hypothesis which claims that the temperature gradient is not directly affected by the radiative structure of the atmosphere.
phi, your post compresses much, and I will not try to respond to most of it. In defence of my point, every debate has rhetorical and substantial aspects. My point here is about the rhetoric, not the substance. I leave the substance for other occasions. The greenhouse gas story is much debated, and the debate has practical effects. The rhetoric is a cogent factor in those effects.
Since you expressed concern about the results of a faster rotating planet being warmer, I inferred you disagreed with it. Maybe you didn’t?
Regarding feedback: As you know, none of the models exhibit net positive feedback in the usual engineering sense. It’s not possible to have a “runaway greenhouse effect” on any planet…it is ultimately limited by T^^4. For years I have dealt with this source of confusion the climate people have created by their not including the Planck effect in “feedback”. And, again, if anyone used Bode theory as an simplifying analogy to the climate system, I wouldn’t be surprised if it’s a poor analogy. I’m not going to spend the time looking at it because it’s irrelevant since the climate models do not depend upon Bode theory.
Maybe they should have come up with a better term than feedback. But what do you call a general process that can either amplify a temperature response, or attenuate a temperature response? “Feedback” is the best term I can think of. If it doesn’t exactly match how feedback operates in electrical circuits…oh well.
Agreed that doesn’t deserve time spent on it. Agreed that climate models don’t use Bode’s theory. But the CAGW advocates such as Michael Schlesinger cite Bode and use his language in an emotively potent and effective turn of rhetoric. I object to that.
well, I don’t have much respect for Schlesinger. But that’s another story. 😉
Responding to your paragraph
Maybe they should have come up with a better term than feedback. But what do you call a general process that can either amplify a temperature response, or attenuate a temperature response? Feedback is the best term I can think of. If it doesnt exactly match how feedback operates in electrical circuitsoh well.
We are talking here about rhetoric, not hard science.
I am not completely certain of the history, but I have read that the term ‘feedback’ was invented by Bode as he sat in the New York ferry on the way to work. He was working on electronic amplifiers for telephone lines. I think the term thence found its way into ordinary language, and now we all use it as such. But in a technical discussion, with Schlesinger explicitly citing Bode, one might ask for the technical meaning as defined by Bode.
Therefore, in this context, instead of ‘feedback’, I would prefer the common scientific parlance of ‘primary’ and ‘secondary’ effects.
The primary effect of added carbon dioxide is increase of optical thickness. It is instantaneous in onset, and far exceeds in importance any other immediate effect such as perhaps a change in the viscosity of the air. One might also allow that the consequent changes in radiative fluxes are primary.
Secondary effects follow, such as changes in temperatures, and then follow changes in water vapour. This ordinary scientific parlance does not invite the melodramatic effect of talk of “positive feedback”, nor the misleading effect of the technical term “amplification”. Instead of ‘amplify’ one can use the ordinary language phrase ‘secondary increase’. If one wants one word instead of two, ‘magnify’ would be less misleading than ‘amplify’.
The quantities are known with such poor accuracy that technical terms such as ‘amplification’ give a spurious impression of precision. Such terms unjustly “lend an air of verisimilitude to an otherwise bald and unconvincing narrative”. That helps the CAGW guys against us.
Maybe. But their terminology will never change. And the terminology doesn’t affect the equations in climate models.
Amongst my mistakes is my above statement that the term ‘feedback’ was invented on the way to work on the New York ferry by Bode. Now I remember that the inventor on the ferry, in 1927 my memory seems to be telling me, was H.S. Black, not Bode. Subsequently, Bode wrote a book about it, Network Analysis and Feedback Amplifier Design, Van Nostrand, 1945, that was cited by Schlesinger.
Obviously I now need to check on the history.
First, I was mistaken to attribute the invention of the term ‘feedback’ to H.S. Black. In 1927, he invented and patented the strategy of negative feedback to improve electronic amplifiers.
The first use of the word ‘feedback’ listed by the Oxford English Dictionary (Oxford University Press) is dated 1920, from the Wireless Age, VIII, 27/1 “An inductive feed-back in relation to the secondary system generates local operations.” This was a technical use, more or less. The Dictionary does not mention Bode’s 1945 book.
The word had entered ordinary language by 1955. It was used in the Times, 31 Aug. 9/4: “Only by constant feed-back from the receptor can one ascertain how far a message has been understood rightly.”
Thus one can say that Dr Spencer is right to use the word as an ordinary language word, without specifically endorsing the Schlesinger usage that cites Bode.
Nevertheless, I don’t like it. It tilts the discussion too easily for the CAGW chaps, giving them a rhetorical advantage, and it isn’t a proper technical usage as is partly implied by the context. It is reasonable to avoid using the word in this way unless one is forced to use it by the opposition or context.
typo: not “local operations”, but rather, “local oscillations”.
“Hanlon’s razor is an aphorism expressed in various ways including “Never attribute to malice that which is adequately explained by stupidity,” or “Don’t assume bad intentions over neglect and misunderstanding.” It recommends a way of eliminating unlikely explanations for a phenomenon (a philosophical razor).”
Though the Left is fundamentally evil. But it’s also just stupid. Violent people of a mob mentally who want to give “peace a chance”.
The problem is relates to trying to understand Venus.
Venus is hotter than “it should be”.
The left has a religion which foolishly assumes that all is known. Science is settled not only in climate science but essential all is known. So that all that needed is experts.
Have totalitarian government run by the guys who know best, and all problems everywhere are solved.
Cuba is on the right track but needs a bit a tweeking to be perfect- or, absolute idiocy.
So Left thinks there is no right and wrong- other the pseudo science of Marxism. Though real Marxism is “misunderstood”.
Criminals are also misunderstood- as are terrorists. And etc.
And the pattern repeats with the Greenhouse Effect theory- people simply don’t understand it.
Anyhow, we can’t have dangerous runaway effect for number of reasons. One reason is we have ocean close to freezing point of water. That alone should be enough stop any panic for thousands of years. Though Lefties do tend to want to solve problems which might arise thousands years in the future- because they are imagining they have the knowledge needed to do so.
Also Venus would be nice place to live- the main problem with living on Venus, is we incapable at the present time of getting off Earth. If living on planet with less than 1 gee were a problem [we don’t know if it is] then Venus could be only habitable planet other than earth in this solar system. If 1/3 gee is habitable, then we got Mars and Mercury which also could be habitable.
Mercury has advantages other than being good place to harvest energy from the Sun. Anyhow Venus is nice place if you want to live in sky cities, but we probably won’t have Venus sky cities within the next hundred [or two] years. The higher priority is getting to point of getting off this lovely planet. This is pretty hard to do, fortunately we have Moon which might be gateway to the rest of solar system.
When one includes clouds as part of greenhouse effect, then it’s very likely the greenhouse effect of our atmosphere is
making Earth a bit warmer. It seems the ozone [btw nothing to do with absorbing longwave IR] also seems to adding to average temperature. The greenhouse gases of H20 and CO2
also seem to have a warming effect. Or I would say they have an effect and that effect is not a cooling effect- doesn’t lower earth average temperature.
Both H20 and CO2 absorb some sunlight- and I don’t think this lowers average temperature of Earth. Both H20 and CO2 are famous for absorbing Longwave IR- and I can’t see how that lowers Earth average temperature. So I would say both gases add some amount to Earth average temperature.
CO2 on Mars freezes it the poles, I think this has warming effect. On Earth H20 freezes everywhere- if at high enough elevation- this likewise has warming effect.
But other than the factor of H2O condensate, and just the radiant effect of H20, I believe just radiant effects cause
earth average temperature to be higher.
I accept that incompetence is to be given precedence over malice or conspiracy, as a possible explanation of things. Still, talk of positive feedback suggests runaway effects, and is thus misleading, and should be called.
It is an advocacy type of science that employs elastic terms which, of course, are stretched to the breaking point. There are real scientific questions that are ignored by the advocates because examination of such questions is detrimental to the advocacy. Best to stick to strechability instead of seeking more definite answers.
It probably goes without saying, but a planet only gets asymptotically warmer as is rotates faster. You can’t get arbitrarily warm by spinning arbitrarily fast. The temperature can do no better than *approach* the effective BB temperature from below.
Hello Dr Spencer,
Thank you for the interesting articles on the temperature of rotating planets.
I was interested enough to develop my own Excel model for a rotating planet, and I got similar results to yours, with a notable exception. My model had the warmest time of day at about 16:00 each day. Your graphs show the warmest time of day to be about 12:00 each day.
I have researched this on the internet, and found the following:
http://www.wisegeek.org/what-is-the-warmest-time-of-the-day.htm
The warmest time of day depends to some extent on precise geographic location, but in most places its somewhere between 3:00 and 6:00 p.m., and the daily high temperature is usually recorded between 5:30 and 6:30 p.m. This is not usually the time of day when the sun is most intense, but intensity and high temperatures dont always go hand in hand. In most places it takes a few hours for the suns rays to be absorbed into the environment, a phenomenon known as thermal response.
I suspect that your day is not starting at midnight.
This does not invalidate the conclusions that you make, only the time of day when the temperatures occur.
My model was specific to the Moon, which has a surface layer with very low thermal conductivity. It thus responds very rapidly to sunlight. The Earth responds more slowly due mostly to the existence of the atmosphere, and partly due to higher conductivity of the soil.
The temperatures of large thermal reservoirs move most slowly, oceans, they even keep their surface warmer at night by convecting upwards.
I’m glad of having realised this circumstance well ahead of someone I admire as much as Roy Spencer. I have been repeating this concept every some time at wattsupwiththat, basically whenever it was relevant for the topic under discussion, like here (2010):
https://wattsupwiththat.com/2010/03/16/another-look-at-climate-sensitivity/#comment-346084
or here (2014):
https://wattsupwiththat.com/2014/02/17/crises-in-climatology/#comment-1571741
I’m pretty sure I mentioned it some additional times but now I cannot find them.
The interesting corollary is that the average temperature of a planet can go up and still its average outgoing radiation could go down (and viceversa). For this to happen, temperatures in cold places or at cold times should go up by a marginally greater amount than temperatures in hot places or times would go down.
Yup! And you are right, the average temperature could go up and the total thermal radiation lost go down. Or, the temperature go down, and the radiation lost go up.
Not at all.
The average is the average – the average is the same everywhere.
If the average energy absorbed per unit area emains the same, the average emitted per unit area remains the same – energy out equals energy in.
Given an average albedo, the average temperature can be calculated. An average. No rotational parameter.
Maybe you meant to say that extremes of hot and cold will be less extreme, asymptotically approaching surface isothermality as revolutions per unit time get very large.
Um…no. Go read the article, it’s very basic.
Um…yes.
It’s very basic.
The idea with nonlinearity of SB equation is very interesting. I strongly agree that the real average temperature on Earth is more an effect of the whole atmosphere than only the greenhouse effect. My experience from Central Europe (where I live) is that the temperature in winter in the early morning strongly depends on the cloud cover: More cloud cover implies warmer mornings. I think that the effect of clouds moving across the surface – covering hot areas and exposing colder areas – must elevate the average temperature, too.
Dr Spencer,
Instead of redefining “feedback”, maybe climatologists could use “normal” scientific terms.
You will quickly discover this is impossible, without appearing foolish.
A bit like coming up with a “normal” falsifiable hypothesis. Cant be done.
Cheers.
“I suspect the effect does not exist if the surface being heated has zero heat capacity”
That would mean that it’s not do with rotation speed.
If the same irradiance that the Moon receives on one side from the Sun was instead directed at the surface in equal measure on the whole surface, the average would be higher, simply because SB is not linear.
The rotation rate effects gains and losses to and from thermal reservoirs.
the average *surface T* would be higher etc..
a semantic distinction. For a real planet (finite heat capacity), the global average surface temperature depends on its rotation rate, especially if there is no atmosphere. Yes, I agree, it has to do with the time lag related to the thermal reservoirs, as I discussed.
Disregarding thermal capacity, if I could take half the solar irradiance hitting the Sun side of Moon and redirect it at the backside, what would the average surface T be then?
Your example is similar to the one I gave, where the planet rotates so fast that, in practical effect, both sides are illuminated at the same time. The average temperature would be warmer.
(Oh, and you can’t “disregard heat capacity”, because it affects the average temperature through its impact on the diurnal range of temperature and thus the nonlinearity impact of the SB equation).
Mine need not be rotating, in fact imagine a case where it is not rotating and has no thermal reservoir. The SB value will be higher than reality purely because the body is theoretically heated uniformly from all directions, as apposed to directionally from the Sun.
Why are you hypothesizing something that’s different from what we are discussing? I’m talking about the effect of diurnal cycle length on the average temperature of a planet. Are you saying such a dependence does not exist? Because Im not sure I can make the explanation any simpler. The longer the diurnal cycle, the greater the diurnal temperature range. The greater the diurnal temperature range, the lower the average planetary temperature due to the T**4 effect.
Yes, Ulric, that is true. It would be the extreme case of no rotation and an infinitely long diurnal cycle, which would maximize the nonlinearity effect. So it’s consistent with what I’ve been saying.
oops! opposed
Your fast switching 1000W example describes something like side of the Moon. It overlooks that half of it always illuminated.
sorry I missed a word again.. like *one* side of the Moon
Moreover, your fast switched example is square wave, that can’t apply to the Moon.
It was a thought experiment, Ulric, make it a sine wave if you want. The conceptual result will be the same. Its no less realistic than your suggestion of a planet that is uniformly illuminated on all sides all the time.
“The greater the diurnal temperature range, the lower the average planetary temperature due to the T**4 effect.”
Due to heat capacity.
“Its no less realistic than your suggestion of a planet that is uniformly illuminated on all sides all the time.”
That’s how you arrived at an average 273K with SB.
True.
273K * 0.25^0.25 = 193K is much nearer to the apparent 213K mean.
That leaves +20K due to the effects of subsoil thermal reservoirs reducing the diurnal range and hence raising the average.
Or I could take a theoretical surface maximum of 394K, and because the illuminated side is spherical and not flat, 394*0.5^.25 = 331.3K, then the average of 331K and around a mean 95K for the dark side is (331+95)/2 = 213K.
Which is why I wanted to factorise the problem by initially disregarding the heat capacity, as it seemed the only sensible way to ascertain how large its effect is, which has to be positive for the Moon.
Ulric, you can’t disregard either heat capacity or the rotation.
The only simple situation is completely uniform incoming light, in which case neither rotation nor heat capacity matters.
For any other distribution of incoming light, both the rotation rate and the heat capacity will affect the average temperature. Increasing the rotation rate would increase the average temperature. Increasing the heat capacity would increase the average temperature. (Up to some asymptotic limit.)
While nonzero heat capacity is necessary for the rotational dependence to exist, that doesn’t mean that it’s a heat capacity effect instead of a rotational effect…because there is no such thing as a planet with no heat capacity. It’s like saying, “a planetary average temperature only exists if there is a planet there”. Well, duh. You could just as easily say it’s an albedo effect because it depends on an albedo less than 1.
My only point was that, for any real world heat capacity, the global average temperature increases with rotation rate. That’s all.
“you cant disregard either heat capacity or the rotation”
I did so temporarily for a good reason, but the calculation was wrong. It is simply 331.3/2.
That the observed equatorial maximum temperatures reach 400K, warmer than the theoretical 394K, could explain why this works out so well without considering albedo:
http://www.drroyspencer.com/2016/09/the-faster-a-planet-rotates-the-warmer-its-average-temperature/#comment-226728
So the average surface temperature for the Moon heated by the Sun on one half, leaving out heat capacity and albedo, is 165.65K, and not 279K. The extra ~47.5K to reach the observed 213K average is the effect of heat capacity, and is half of the average cold side temperature.
How come everyone has been misapplying SB on this for so long without realising?
Nikolov & Zeller saw the problem with way S-B has been applied, but failed to find the correct solution.
For an Earth value with no heat capacity and 0.7 albedo, the illuminated side would be 331.3K*(0.7^0.25) = 303K, giving a cold side T of 273K for a global average of 288K. Implying that whatever additional heat capacity or greenhouse effects that are in practice reducing that diurnal range, must be reducing the average daytime temperature. Unlike the Moon where equatorial temperatures can climb above the theoretical 394K.
Or rather “giving a cold side T of 273K for a global average of 288K” once heat capacity is allowed.
and typo.. 0.3 albedo.
“How come everyone has been misapplying SB on this for so long without realising?”
They haven’t been. For example, in Ray Pierrehumbert’s book, he notes that applying the SB formula works out well for a planet that is at a pretty uniform temperature…But, if the planet has the combination of a low enough heat capacity and slow enough rotation that there are large variations in the surface temperature, then it will not work. But, as he points out, an average temperature for such a planet isn’t that much of a useful concept anyway when the variations are so extreme.
“Nikolov & Zeller saw the problem with way S-B has been applied, but failed to find the correct solution.”
They didn’t discover anything that scientists didn’t already know. They just rediscovered it and are acting like they have discovered something very new and important. (To be fair, I suppose you can argue that they brought this point to a broader non-scientific audience, although they have also done this audience a disservice by saying lots of things that are just plain wrong.
Joel Shore, yes it has been misapplied, as my calculation of Lunar temperatures shows. S-B can only be applied to the illuminate hemisphere, not to the whole sphere.
Joel writes:
“..although they have also done this audience a disservice by saying lots of things that are just plain wrong.”
Yes I agree with that fully. But think what greater disservice has been done by the illegitimate application of S-B. An increase in the water vapour greenhouse effect on Earth reduces the average daytime side temperature.
Tim says:
“Increasing the rotation rate would increase the average temperature.”
The cold side of the Moon would not have so long to cool down if the rotation was faster, but then the regolith would also have less time to heat up again.
Tim says:
“Increasing the heat capacity would increase the average temperature.”
Of course, without heat capacity the average surface temperature of the Moon would be colder by 0.5 of the average temperature of the cold side.
Colder by 0.5 of the *real observed* average temperature of the cold side, just in case you didn’t follow that.
The uniformly heated blackbody is 394K divided by root 2, 394/1.414213 = 278.6K.
The blackbody heated directionally on one hemisphere is 394 divided by the fourth root of 2, 394/1.1892 = 331.3139K, but only for that hemisphere, the global average is half of that, aside from the 3K background radiation.
Roy says:
“While nonzero heat capacity is necessary for the rotational dependence to exist, that doesnt mean that its a heat capacity effect instead of a rotational effectbecause there is no such thing as a planet with no heat capacity.”
It would depend on whether or not the heat sinks are reducing the potential surface temperature of the heated hemisphere.
“The reason is very simple, and is related to the non-linearity of the Stefan-Boltzmann equation, which can be used to estimate how warm a body gets based upon the rate at which it absorbs solar energy when its only mechanism to cool is through thermal emission of radiation:”
Roy…this article presents and excellent, concise analysis of Stephan-Boltzmann as applied to the greenhouse effect. It concludes that radiation is immaterial.
Before anyone starts ad homming this paper as having been debunked, I have read all the alleged debunking papers and not one comes close to the elegance with which this paper is presented. The first, by Arthur Smith, a physicist who has worked his entire career as a librarian, attacked only one part of the paper regarding the difference of 33C in temperature between an Earth with no atmosphere or oceans and and Earth with both. His paper was attacked by a third party who disproved his allegations.
The second, by Halpern et al, were stymied by a misunderstanding of the difference between EM radiation and heat with regard to the 2nd law. They alleged that G&T had claimed only one radiator in a system with two radiating bodies was radiating. That was in response to the claim by G&T that the 2nd law required heat transfer in one direction only.
https://arxiv.org/PS_cache/arxiv/pdf/0707/0707.1161v4.pdf
See page 19, although it’s worth reading from the beginning of the chapter.
Conclusions:
“Three facts should be emphasized here:
-In classical radiation theory radiation is not described by a vector field assigning to every space point a corresponding vector. Rather, with each point of space many rays are associated. This is in sharp contrast to the modern description of the radiation field as an electromagnetic field with the Poynting vector field as the relevant quantity.
-The constant (sigma) appearing in the T4 law is not a universal constant of physics. It strongly depends on the particular geometry of the problem considered.
-The T4-law will no longer hold if one integrates only over a filtered spectrum, appropriate to real world situations.
I think Roy has agreed with point 3”.
What a crock! G&T’s paper is utter garbage.
(1) I know Arthur Smith…We went to grad school together at one of the top physics grad schools in the nation. And, Arthur is not a “librarian”. He works for the American Physical Society as “Lead Data Analyst”, also described as an IT manager. And, even though he (like I) did not pursue a career in academic research, I would bet that his publication record (https://scholar.google.com/citations?user=UU8jK4EAAAAJ) still stands out compared to G&T.
(2) The paper by Halpern et al., of which I was a co-author, demonstrated explicitly using simple models (such as Roy Spencer is using here) how the greenhouse effect operates and how there is no violation of the 2nd Law because the heat flow is always from hotter to colder. There were a few cases in that paper where we used unfortunate terminology of talking about heat flowing in both directions where we should have more properly said the radiation is in both directions, whereas the heat (net macroscopic energy flow) is from hot to cold. Such poor word choice is easily cured by making a few word substitutions in the paper…and such change has zero impact on the argument or conclusions, which of course, were based not on our words but on our calculations. And, G&T did indeed ignore the greater radiation being transferred from the Earth to atmosphere in concluding that the greenhouse effect violates the 2nd Law. That is the only way that they could possibly come to that idiotic conclusion.
More snippets from G&T (sorry, have to break it into parts since the site filters won’t accept some words):
-page 16…Heat is the kinetic energy of molecules and atoms and will be transferred by contact or radiation.
My note: this agrees with Clausius and both G&T have expertise in thermodynamics, Gerlich as a math teacher in the field and Tscheuschner as a researcher.
-page 22…a larger portion of the incoming sunlight lies in the infrared range than in the visible range. In most papers discussing the supposed greenhouse effect this important fact is completely ignored.
my note: incoming solar radiation is 45.2% from the IR band as opposed to 44.8 from the visible band. Surely some of that IR heats GHGs in the atmosphere.
More snippets from G&T (continued):
-page 32…they describe the Woods experiment of 1909 and quote the exact Words of Woods. Woods sums up:
“Is it therefore necessary to pay attention to trapped radiation in deducing the temperature of a planet as affected by its atmosphere? The solar rays penetrate the atmosphere, warm the ground which in turn warms the atmosphere by contact and by convection currents. The heat received is thus stored up in the atmosphere, remaining there on account of the very low radiating power of a gas. It seems to me very doubtful if the atmosphere is warmed to any great extent by absorbing the radiation from the ground, even under the most favourable conditions”.
Its good that you brought readers attention to the paper by G&T
Their analysis has yet to be be contradicted by any serious challenger.
The paper above (co-authored by Joel Shore) could not even master the technical language of thermodynamics.
G&T replied with
https://arxiv.org/abs/1012.0421
Readers will form their own opinion.
I for one find myself in agreement with James Lovelock who now finds Global Warming alarmists to be little more than members of a new religious cult
Only in the bizarro world of Bryan is it the case that it is fine to be totally wrong on the science as long as you don’t make any mistakes in the words you use to describe it, spelling, or punctuation.
If energy out equals energy in, and spinning a body doesn’t increase its energy absorbing ability, then the average temperature remains unchanged, regardless of spin.
Alternatively, spinning a body causes it to absorb more energy, and its temperature to rise.
I’m pretty sure the second is nonsensical, thought experiment or not.
Cheers.
You miss the whole point of the post.
Have you ever done a surface integral????
Let’s do a simple example. Compare the total radiative output of a body (let’s call it a blackbody for simplicity) uniformly at 255K to one that is half at 355K and half at 155K.
Ed Bo,
What part of my statement are you disagreeing with?
What you propose is as silly as saying that the area of a right triangle with sides 5.5 , 12, and 13 is anything at all. All your calculations are meaningless.
And so with your example.
If, as Trenberth says, the Moon receives an AVERAGE of 341.3 W/m2, then if there is an AVERAGE albedo, an AVERAGE amount of energy is absorbed for every square meter of the TOTAL surface. This is exactly counterbalanced by the AVERAGE emitted energy for every square meter of the Moon’s surface. You cannot emit more than you receive.
What has rotation to do with anything? From memory, surface integrals don’t concern themselves with whether the surface is moving or not. It’s irrelevant.
Cheers.
Mike did you even read the original post? Every square meter has its own absorbed solar energy and resulting emitted energy, but they are almost never in balance locally because of the diurnal cycle combined with finite heat capacity of the surface.
Because the relationship between absorbed solar (or emitted IR) and temperature is nonlinear through the S-B equation, the rotation rate, and thus length of the day-night cycle, affects the day night temperature difference, and thus how far out you are on the cold and warm ends of the nonlinear S-B curve. As a result, the length of day affects the global area average temperature.
Dr Spencer,
You wrote –
“Imagine a body with a realistic heat capacity that uniformly absorbs a solar intensity of 1,000 Watts per sq. meter for 1 second, then 0 W/m2 for one second, over and over. Think of it as a 2 sec long diurnal cycle. That rapidly flickering energy source would be too fast for the temperature. to come into equilibrium with the absorbed sunlight (or lack of sunlight). It would, in effect, be like a continuous energy source of 500 W/m2 in intensity, and the resulting S-B temperature (assuming a thermal radiative emissivity of 1.0) would be about 307 Kelvin, taken from the curve in Fig. 1.”
Unfortunately, the Moon, or any similar body, absorbs “solar” radiation from one direction only. Talk of “uniformly absorbing” is incorrect. One hemisphere is absorbing, one hemisphere is radiating.
A square meter normal to the Sun will be exposed to around 1370 W. A square meter at the polar terminator will be exposed to almost zero – the rays will be almost parallel to the surface.
Any point on the surface spends equal time on the lit and unlit sides.
Speeding the rotation of the globe means that a point on the lit side will not heat as much, having less time to absorb a fixed amount of energy. And on the unlit side, the converse.
With very high rates of rotation, a point at any latitude would approach isothermality for that latitude. The equatorial regions would still be hotter than the poles, due to the incident angle of the radiation.
Given an average emissivity of 0.9, an average input energy of 341 W/m2, and the application of Kirchoff’s law, the AVERAGE temperature over the whole of the Moon’s surface is around 286 K.
I would be happy to be corrected if I have erred in fact.
Cheers.
It strikes me that looking for reasons why the Moon is colder than you think it should be, while knowing that is warmer than it would otherwise be because of its heat capacity, is like making 2+2 = 0.25.
*it* is warmer etc
Dr Spencer,
Consider a perfectly reflective sphere made of impossibilium (atomic number 9 and 3/4).
Spin away! Makes precisely no difference to a perfectly reflective sphere.
Or try impossibilium subjected to back radiation from N rays. This has a perfectly absorbent surface, and is capable of instantaneously transferring heat within its body. This ensures perfect isothermally. No part can be at a different temperature than any other part.
Spin away! Makes no difference to surface temperature.
Or take a real sphere “uniformly” (your words) absorbing energy. This would be in the depths of space, and the sphere would achieve a temperature equal to that of the environment – around 3.7 K.
Spin away! The temperature remains the same.
You say “The Faster a Planet Rotates, the Warmer its Average Temperature”.
I disagree. I think I’m right.
Cheers.
Sorry. Isothermally.
Cheers.
Arrgh!
Isothermality!!!!
Cheers.
You are not correct.
Two different temperature distributions that give the same average temperature can have a different average T**4 and hence a different emission. Conversely, two different temperature distributions that give the same emission because they have the same average value of T**4 can have a different average temperature.
The temperature distribution is a function of the spin rate because a planet that spins very slowly will have a broader distribution of temperatures whereas one that spins more rapidly will have a narrower distribution of temperatures.
A broader distribution of temperatures leads to a lower average temperature because of a mathematical theorem called Holder’s Inequality that says that the average of T for any distribution of temperature T is always less than or equal to the fourth root of the average of T**4.
It is easy to see this with simple examples: For example, consider a planet that has a uniform distribution of temperature with an average temperature of 200 K and compare that to a planet that has a distribution such that half of it is at 0 K and half at 400 K (and hence also has an average temperature of 200 K). You will find that the planet with the uneven distribution emits more radiation than the one that is uniform.
[The spam filter is flagging part of my post…so I am trying to figure out what in this first paragraph is being rejected.] The average temperature for a body is that necessary to have the energy emitted equal the energy absorbed.
Joel Shore,
The Moon absorbs energy from the Sun.
It manages to get rid of it all, plus a wee bit of its own residual heat.
Spin it round, up, down, or sideways. Ignoring the Moon’s gradual cooling, energy out equals energy in.
Energy in comes from the Sun. You seem to be claiming that you can prevent energy leaving an object, and hence warming, by rotating it!
Maybe you’re using sticky climatological heat, rather than normal heat.
Good luck with that!
Cheers.
Mike,
I thought you were honestly trying to learn. Not it is clear that you want to remain ignorant. One cannot cure ignorance unless it wants to be cured.
Believe whatever nonsense you want to believe.
“any process which increases the day-night temperature range (such as a longer diurnal cycle) will decrease the average temperature of a planet, simply because of the non-linearity of the S-B equation.”
Dr. Spencer, this is due to derivative of the S-B equation with respect to temperature
J = e o T^4
dJ/dT = 4 e o T^3
Hence, the higher the temperature, the more energy is needed to increase the temperature. Longer day has higher maximum temperature and needs more energy. Since energy input is equal in both cases (long-day-night and short-day-night) the average temperature of the long-day-night is lower.
The above differential equation is similar to Debye law where the specific heat is proportional to the cube of temperature
Cv = a T^3
Where Cv is specific heat and a is a constant
I always thought day equals night no matter how fast a planet spins. The amount of insolation always equals the amount of non-insolation.
Whether or not there is an atmosphere?…things become a little more strange. Suddenly there is no atmospheric “surface temperature” as we know it here, (average), ie no temperature reading from where a Stevenson screen would be situated, none, zilch, because you’re in space. The “surface temp” would have to be taken with the thermometer right on the ground….and we know that ball of rock in space orbiting the Sun, at the same distance, would get instantly scorching hot at sun rise, and freeze in seconds at sunset. Averaging those temperatures would give a mean somewhere in the middle of those extremes…no hotter..no colder….for the planet with no atmosphere.
This atmosphere-no atmosphere nonsense has got to stop.
“The surface temp would have to be taken with the thermometer right on the ground.and we know that ball of rock in space orbiting the Sun, at the same distance, would get instantly scorching hot at sun rise, and freeze in seconds at sunset. ”
At noon when sun near zenith clear day, one earth sun is about 1000 watts per square meter of direct sunlight [if combined with indirect sunlight it is 1120 watts per square meter {wiki, sunlight}]. With a rock without atmosphere [like the Moon] the sunlight is about 1360 watts per square meter [all of it direct sunlight- no indirect sunlight].
With a rock without atmosphere the sunlight is similar to Earth’s sunlight [and one characterize the sun on Earth as “scorching”] a main difference would be the Earth atmosphere prevent some of the sun’s UV and X-rays, but roughly it warms say a frying pan the same. When earth air is warmer a frying pan could be warmed as much as, say 70 C, and would take about hour to warm up. With moon without atmosphere, the same frying pan would take also about hour to warm up to about 120 C.
In terms of cooling, if heat a frying pan to 120 C and put outside, it will cool roughly as quickly as 120 C frying pan on Moon shaded from the energy sunlight.
But with the moon, it has 14 days to our 12 hours of daylight, or our last hour of daylight is equal to about +24
hour of late afternoon sunlight on the moon.
And even with the 1360 watt per square sunlight, it has very little ability to warm if the sun is at low angle to it. Or, yes, even before the sun sets, the lunar surface is freezing.
Or “days” before sunset when sun is say 30 degree above flat surface, it’s about 1360 / 2 – being about 680 watts per square meter. Also on Earth when sun is lower than 30 degree above horizon, it does not have much direst sunlight and the level ground will not heat up much.
You check this out any day- measure sidewalk temperature near noon and compared to when there is less than 2 hours of sunlight in the day.
You’ve got an uncanny knack of taking a straight forward, easily understandable, logical explanation of something, and then totally buggerising it with a mindless, meandering,conglomerate of numbers, calculations and thought processes, which eventually wind to a halt, leaving the reader in the end to wonder what the hell was the object of the exercise in reading your verbose offering.
Make sure you visit Roy’s 2+2=4 posting.
“Youve got an uncanny knack of taking a straight forward, easily understandable, logical explanation of something, and then totally buggerising it with a mindless, meandering,conglomerate of numbers, calculations and thought processes, which eventually wind to a halt, leaving the reader in the end to wonder what the hell was the object of the exercise in reading your verbose offering.”
Well, that could one way to look at it.
If when the Moon has the sun blocked by Earth, and the surface
cools by about 100 K within two hours- 120 C to about 20 C.
Is rapid, then Moon rapidly cools and warms.
But if Earth were similarly blocked [by something big- not small like the Moon] I would expect a 70 C surface to cold by +50 K within 2 hours of complete darkness.
If that is slow or normal, or not instantaneous, fine.
But the main reason the Moon is below freezing [less than 0 C] before the sun goes down is because it has slow rotate AND
because when sun is about 5 degree above the horizon, one has about 1/11th the amount of sunlight per square meter on the level surface.
Or 1360 / 11 is 126 watts per square meter.
Or 240 watts per square meter warms a surface to about -18 C. Or one get around 240 watts when sun is close to 10 degree above the horizon.
Of course if standing up and thereby facing the sun, when sun at 5 degrees above horizon on the Moon and facing the sun, one gets 1360 watts per square meter.
Away goes gblaikie again, blathering on about the Moon.
Where did I ever make mention of the Moon in my comment?.
A fun fact, perhaps, is that the nearest rock in which it’s rocky surface is in a vacuum, would be the Moon.
Give yourself a pat on the back, Blaikie. You’ve made a comment of only one sentence.
A more distance rock is the dwarf planet Ceres.
“The study also shows that daytime surface temperatures on Ceres span from minus 136 degrees to minus 28 degrees Fahrenheit (180 to 240 Kelvin). The maximum temperatures were measured in the equatorial region.”
http://www.nasa.gov/feature/jpl/dawn/new-clues-to-ceres-bright-spots-and-origins
Ceres has rotation period of about 9 hours
And Ceres receives about 1/10th of Earth distance sunlight-
130 to 140 watts per square meter.
So this rock has 9 hour day and 240 K surface temperature at equator.
Also has some kind of atmosphere- probably safe to say more atmosphere than the Moon [it’s has pretty good vacuum].
I don’t know what the nighttime temperature of Ceres is at the equator. Or how much the equator cools from it’s 240 K
surface temperature at noon.
Let suppose it’s somewhere around the Moon night time equatorial temperature which about 95 K or it cools by about
145 K.
If it was 95 K what would that mean in terms of Ceres having atmosphere. Or say instead it was 140 K- cooled only 100 K from noon highest temperature- what does that indicate in terms of how atmosphere Ceres might have?.
And How would factor length of day- daylight is 4 1/2 hours, and from around noon it’s about 2 hours to evening.
Or at “3 pm” when sun about 45 degree above horizon, it’s an about hour before sunset and then another 4 1/2 hours
before dawn.
I think with the Moon, its rotation would have to be slowed down much closer to synchronous rotation with the Sun for its heat sinks to retard warming rates at the surface. Or alternatively speed it up considerably so that the sunlit does not reach equilibrium with the solar irradiance. There should be a wide band in between those extremes where changing the rotation rate makes little difference.
sunlit *side*
A more dominating force is earth’s graviational force.
The Moon is tidally locked with Earth- same side faces Earth and rotates relative to Sun with it’s orbital period with Earth.
Earth is not tidally locked with the Moon and the effect of Earth rotation relative to the Moon’s gravity is the earth’s ocean tides. The tidal effect of the moon [which can combine with the Sun’s gravity- spring tides- “Spring tides occur when the moon is either new or full, and the sun, the moon, and the Earth are aligned.”-http://www.thefreedictionary.com/spring+tide ]
in addition effecting the ocean also effects rocky surface of
Earth {by small measurable amount].
The Moon’s spherical mass is also not uniform and this is another factor [see gravitational gradient] which makes one side of the Moon face the Earth.
Dr. Roy Spencer,
Simple question. If I accept that faster rotation leads to increased temperature, for a body without an atmosphere; how would this change if you simply added a generic atmosphere? Would the atmosphere simply mitigate the temperature difference between day/night? Would this then come more in line with average temperature of a slower rotating body?
Also, what would be theoretical limits? I. Other words, would a planet rotating infinitely fast gain infinite heat? Would a infinitely fast rotation have a terminal heat gain? Thinking along that same line, would a planet rotating just slightly faster than being tidally locked, see any realistic average temperature gain?
Many thanks!
Ken D:
“Simple question. If I accept that faster rotation leads to increased temperature, for a body without an atmosphere; how would this change if you simply added a generic atmosphere? Would the atmosphere simply mitigate the temperature difference between day/night? Would this then come more in line with average temperature of a slower rotating body?”
When we consider Earth without-atmosphere and Earth with atmosphere the difference will be very small. I calculated Earth’s average surface temperature with atmosphere
being higher from T = 288 K by only about 0,4oC.
Ken D:
“Also, what would be theoretical limits? I. Other words, would a planet rotating infinitely fast gain infinite heat? Would a infinitely fast rotation have a terminal heat gain? Thinking along that same line, would a planet rotating just slightly faster than being tidally locked, see any realistic average temperature gain?”
I discovered that PLANETS MEAN SURFACE TEMPERATURES, everything else equals, relate as the 16th root of their rotational spin.
Example:
Assume we have a planet with N = 1 rotation /day and
Tmean = 300 K
Thus, for a very slow rotational spin, say,
N = 0.0000000000000001 rotations /day
the 16th root will be 0,1 – which gives us 0,1Tmean compared to the planet with N = 1 rot /day (everything else equals),
or Tmean = 0.1 *300 K = 30 K
Now, for a very fast rotational spin, say,
N = 10,000,000,000,000,000 rot /day (everything else equals)
the 16th root will be 10 – which gives us 10Tmean compared to the planet with N = 1 rot /day (everything else equals),
or Tmean = 10 *300 K = 3000 K
But these are extremes, there are not planets with so extreme rotational spins.
Lets have N = 100 rot /day – the 16th root is 1.334
and the temperature will be 1.334 *300 K = 400.06 K
And let’s have N = 0,001 rot /day – the 16th root is 0.649
and the temperature will be 0.649 *300 K = 194.81 K
https://www.cristos-vournas.com
The temperature of a planet is not a function of rotation. The temperature remains constant no matter how fast it spins.
Let all T’s be the temperature raised to the fourth power. Let Ts be the hot source temperature. Let Th be the planet’s hot side temperature. Let Tc be the planet’s cold side temperature. k is the Stefan-Boltzman constant x emissivity. Start with a non-rotating planet at steady-state. From the Stefan-Boltzman equation”
Heat absorbed on the hot side = k(Ts – Th)
Heat emitted on the cold side = kTc
at steady-state k(Ts – Th) = kTc
Therefore, Tc = Ts – Th
Rotate the planet 180 degrees so the cold side faces the sun and the hot side faces outer space.
heat absorbed on the hotside = k(Ts – Tc), but Tc = Ts – Th
heat absorbed on the hotside = kTh
heat emitted on the cold side = kTh
heat absorbed on the hot side = heat emitted on the cold side. The planet remains in energy balance and the temperature of the planet can not change.
As you rotate the planet, and an increment of cold side faces the sun, the same amount of hot side faces outer space. The planet remains in energy balance and no matter how fast you rotate the planet, its temperature will not change.
I would of thought factors like dams, buildings, and wind farms providing friction and pressure differentials in the boundary layer would slow the Earths rotation and have a warming. Rossby waves from the Earths rotation and Coriolis effect are already stronger in the said Northern hemisphere due to more land, the highest mountains, and more land sea boundaries. Rossby waves are linked to extreme weather and amplified warming of the Arctic as well as destabilising the polar vortex preventing stratospheric clouds from forming a prerequisite for solar wind depleting the ozone layer after Solar dawn in Spring.