Home/BlogABSTRACT
While the non-linearity of the Stefan-Boltzmann equation leads to at least a 60 deg. C overestimate of the Moon’s average surface temperature if a global-average solar flux is used in place of computing temperatures over a sphere with a diurnal cycle, the error is only about 5 deg. C for the Earth. The difference is due the the very long lunar day (29.5 Earth days), which causes a very large diurnal cycle in temperature, which enhances the errors arising from the nonlinearity of the S-B equation.
The greenhouse effect is often claimed to cause an average warming of the Earth’s surface of about 33 deg. C, from an atmosphere-free value of about 255 K to the observed value of around 288 K. In the no-atmosphere case, the absorbed solar flux heats the surface up until the thermal emission of longwave radiation matches the intensity of absorbed sunlight.
Typically this theoretical average surface temperature is computed using a global average of the absorbed solar flux, and then using the Stefan-Boltzmann equation to find the emitting temperature that matches it.
But the strong nonlinearity of how the S-B flux depends upon temperature can lead to a warm bias in the no-atmosphere temperature estimate if a wide range of solar fluxes are used in a single average:
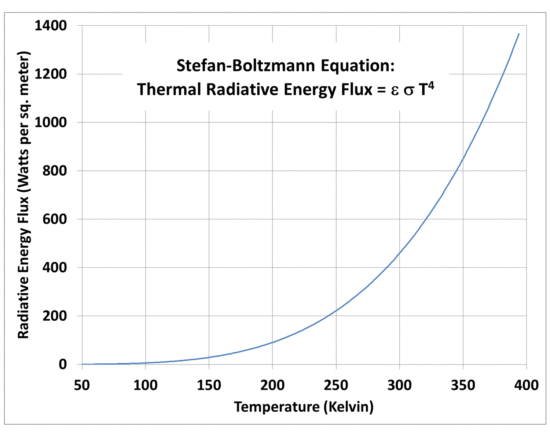
Fig. 1. The non-linearity of the Stefan-Boltzmann equation leads to a warm bias if a global average solar flux is used to estimate a global average equivalent emitting temperature.
If the absorbed solar flux does not vary much over the spherical shape of a planet without an atmosphere, then using a global-average solar flux will give a pretty good estimate of the global average surface temperature.
But the absorbed solar flux actually varies a lot over a spherical planet.
So, just how large of an error is introduced by the use of a global average flux to calculate an average temperature? (My recent discussions with David South, an Auburn forestry professor, led me to reexamine this issue.)
In the case of the Moon, the error is very large. As has been pointed out elsewhere (e.g. by Willis Eschenbach here, and Nikolov & Zeller here), extreme day-night temperature swings on the Moon can cause a single-solar flux estimate of surface temperature to be biased very high, due to the nonlinearity of the S-B equation. The error can be many tens of degrees C.
Clearly, the 33 deg. C estimate for the Earth’s atmospheric greenhouse effect depends upon how accurate our estimate is of the average surface temperature of the Earth without an atmosphere. (I won’t go into the reasons why we really don’t know what the Earth would look like without an atmosphere, which affects it’s albedo and thus how much sunlight it would absorb, which in turn will impact the temperature calculation).
Since the non-linearity induced error depends upon just how hot surface temperature gets during the daytime, you need to do the calculations using a diurnal cycle, including how deep the solar heating (and nighttime cooling) penetrates into the surface. Also, obviously, the calculations need to be done on a sphere.
So, I put together this model spreadsheet that allows you to change planets (through the assumed solar irradiance), the assumed solar albedo of the atmosphere-free planet, surface longwave emissivity, and how deep of a water/soil layer is assumed to change in its temperature in response to imbalances between absorbed sunlight and thermally-emitted longwave radiation.
The time-dependent calculations are done in 96 increments of a day, which is 15 minutes for the Earth, at latitudes of 5, 15, 25, 35, 45, 55, 65, 75, and 85 degrees separately at assumed equinox conditions. Cosine latitude weighting then gives a pretty good estimate of the area averaged temperature over the sphere. It can take up to a couple weeks for the polar regions to finally equilibrate when the model is initialized at absolute zero temperature. The plots that follow are after 40 day-night cycles of the model run.
When I run the model for the Moon, which has a 29.5 Earth-day diurnal cycle, I found that I needed a soil layer of about 0.05 meters depth (about 2 inches) to match actual temperature measurements on the Moon (see Willis’s post here for some actual lunar temperature measurements). This is the thickness of soil assumed to be uniform in temperature that responds to solar heating and IR cooling. Of course, in reality the very top of the soil surface will get the hottest/coldest, with the temperature swings dampening strongly with depth; the model just uses a thin, uniform-temperature layer that approximates the average behavior of the real, thicker layer.
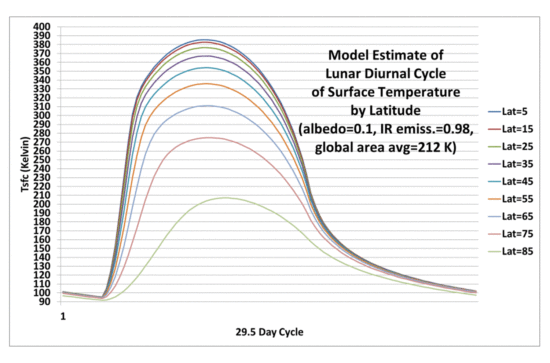
Fig. 2. Diurnal cycle in lunar surface temperatures at different latitudes calculated from a simple time-dependent model during equinox conditions.
Significantly, the resulting global area average lunar temperature of 212 K is 61 K colder than the 273 K one gets by just putting the global average absorbed solar flux through the S-B equation to get a single temperature. As discussed by Willis, this shows the large bias that can result from S-B equation calculations when one doesn’t bother to average over a wide range of temperatures.
So, How Large is the S-B Bias in Earth Temperature Calculations?
Just how big is this warm bias effect when computing what the Earth’s global average surface temperature would be in the absence of an atmosphere?
If I repeat the model calculations in Fig. 2 and only change the length of the diurnal cycle, from 29.5 Earth days (for the Moon) to 1 day, we get (obviously) a greatly reduced diurnal range in temperature (22 deg. C diurnal range, global average, versus 209 deg. C diurnal range for the Moon), and a global average surface temperature of 267 K. This is only 6 deg. below the 273 K value using a single solar flux in the S-B equation:
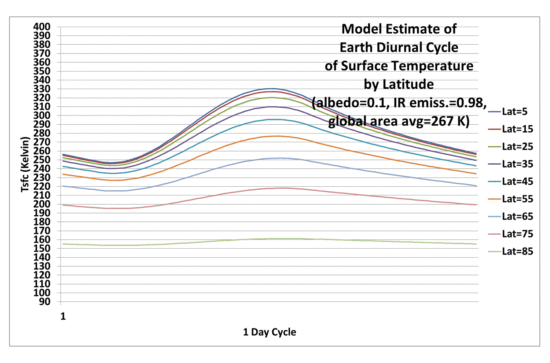
Fig. 3. As in Fig. 2, but with a 24 hr (Earth) diurnal cycle rather than 29.5 days (lunar diurnal cycle).
If I use the more traditionally-used Earth albedo value of 0.3, I get a global average surface temperature of 251 K, which is only 5 deg. C below the single solar flux calculation of 256 K. Thus, the error caused by using a single global average solar flux to estimate a global average terrestrial temperature in the S-B equation is much less for the Earth than it is for the Moon.
Fig. 4. As in Fig. 3, but using a solar albedo of 0.3 rather than 0.1.
Conclusion
Using the S-B equation with a global average absorbed solar flux to compute the global average emitting temperature of the Moon leads to a very large warm bias, as reported by others.
But that lunar bias (about 60 deg. C) is mostly due to the very long period of daylight on the moon, which is 29.5 times longer than on Earth. When the Earth’s diurnal cycle length is used, the warm bias is only about 5 deg. C.
One might then wonder if this means that the 33 deg. C greenhouse effect on Earth should really be 38 deg. C?
Maybe…but I would say that the 33 deg. C number is suspect anyway. First, because it depends upon an albedo of 0.3, which is probably too high. If I use a lunar albedo for the Earth, then the GHE becomes only 21 deg. C with the new calculations. One might wonder if the no-atmosphere Earth would be ice covered, with a very high albedo and very low surface temperatures, but the existence of water would lead to evaporation/sublimation, and a water vapor atmosphere. So an ice Earth is, I believe, incompatible with the assumption of no atmosphere. But I’m open to different arguments on this point.
Secondly, the 33 deg. C number isnt really the greenhouse effect, anyway. It’s more of a total “atmosphere effect”, the final result after atmospheric convection has cooled the surface substantially below the very high temperatures the greenhouse effect would cause in the case of pure radiative equilibrium (see Manabe and Strickler, 1964).
So, you can get a wide variety of numbers for the estimated surface warming effect of the atmosphere (combined effect of greenhouse warming and convective cooling). They depend on what assumptions you make in your calculations related to what an atmosphere-free Earth would look like, which are at the very least uncertain, and at most, physically impossible.
The bottom line, though, is that neglect of the nonlinearity of the S-B equation leads to about a 5 deg. C overestimate of the average surface temperature of the Earth in the absence of an atmosphere.
NOTE: Most of the comments on this post will likely be off-topic, centering around the extreme minority view of a few people that there is no atmospheric “greenhouse effect” involving the atmosphere emitting infrared radiation toward the surface.
Does the 4th root of the average of the 4th power of the actual surface temperatures at the various points on the moon equal the predicted temperature if the temperature would be uniform over the whole moon?
If I understand your question, then Yes.
No. The SB Law cannot account for the temperature of the dark side of the moon — that depends on thermal conductance through the lunar regolith.
Roy,
We have a 21-page published paper in SpringerPlus on the proper method for calculating the temperature of an airless body that discusses in details all aspects of the issue:
https://springerplus.springeropen.com/articles/10.1186/2193-1801-3-723
PDF file is also available here:
https://tallbloke.files.wordpress.com/2016/09/ge_magnitude_volokin_rellez_2193-1801-3-723_springerplus_2014.pdf
Please use this paper as a reference in the future instead of the non-peer-reviewed blog articles from several years ago!
Thank you!
Hi Ned:
From what I read in the first paper you reference, it sounds like the authors argue that the planetary rotation rate does not matter much for calculating the global average temperature.
But from my analysis here, it matters a great deal! The longer daylight lasts, the higher the surface temperature, which then leads to much more efficient loss of thermal radiation to balance incoming solar.
As a result, just the change in rotation rate between the Earth (1 day) and Moon (29.5 days) leads in my calculation to a global average temperature difference of 55 deg. C (!)
-Roy
Hi Roy,
Yes, I’m well aware that models oftentimes simulate an effect of rotation rates on global temperature. However, the empirical data do not show such effects.
If you read our second paper describing an accurate empirical model of the average global near-surface temperature derived data of planetary bodies spanning a huge range of environments, you will notice that the model does not account for differences in rotation rates. Yet it performs remarkably well despite the fact that the 6 studied bodies have rotation rates ranging from 1 day (Earth) to 243 days (Venus):
https://tallbloke.files.wordpress.com/2016/09/planetary_temperature_model_volokin_rellez_2015.pdf
This suggests that we need to find out why models predict an effect of rotation when none is visible in the data.
Empirical data would require rotating spheres with no-atmosphere be compared. Your two examples have atmospheres.
Perhaps albedo is the answer. Atmospheres with high albedo are poor radiators so diurnal temperature swings would be muted.
If body can absorb the sunlight then it matters less what rotation rates is.
The Moon does not absorb the sunlight, well.
Or the Moon can have sunlight [1360 watts per square] shining on it for 40 hours and 1 meter below the surface it can be -30 C. So in minutes top inch of surface can warm from -100 C to 100 C, but because of material and it being vacuum, it’s has very good insulative properties- and so Lunar surface absorbs very little heat.
Were there a bare rock on lunar surface, it would heat like a rock would on Earth- not real fast, but much faster the dusty surface [3 or 4 “] which entirely covers the lunar surface.
Were you place a block of metal on the Moon, it could more quickly absorb the energy of the sun as compared to a bare rock. Or a meter thick chunk of copper could absorb a lot of energy. And if painted it white it would not reduce how much it absorbed by very much.
Not quite. The Moon absorbs 90% of the sunlight that falls on it. Low thermal conductivity of the surface means it gets even hotter in daylight, which magnifies the nonlinear IR loss effect, and reduces average lunar temperatures over the full day/night cycle.
Ned: You are still wrong. Standard radiative physics completely accounts for the temperature of the lunar surface. The (simple) calculation is here:
http://davidappell.blogspot.com/2012/04/norfolk-constabulary-made-wrong-charges.html
C’mon Roy, you know fluxes must balance at eqm. Rotation does not alter the fact that a sphere cuts a circle out of a parallel flux but still emits as a sphere, whether it rotates or not the effective mean radiative temperature is unaffected.
Gee this mens that Geoff’s the effective mean radiative temperature is some calculation of a temperature where the incoming and outgoing average powers are equal regardless of what local temperatures may be or how great the variance changes with rotation rate. In other words if you statistically merge enough stuff together the result is meaningless!
I noticed that NASA took a picture of Titan showing what it claims are water plumes spouting very high up into the atmosphere. Does Titan have a water vapor atmosphere? I have no idea but it may prove your point.
RE the 33C “Its more of a total ‘atmosphere effect'”
Sure, convection, clouds, and GHGs included.
I compared monthly emissive temperatures ( solving S-B for T on CERES OLR ) for monthly surface temperature and I think the result is elucidating. While this is the ‘total effect’ and it’s dominated by the NH seasonal cycle, it does demonstrate the 33C, demonstrates positive feedback, but also demonstrates that GAT varies by about 5C every six months without the world ending:
http://climatewatcher.webs.com/TE_SFCT.png
Dr Roy,
Your exercise led me to wonder how much the slowing of the earths rotation over the centuries would have affected the earths temperature. I learned that over the last 620 million years the earths length of day is thought to have gone from 22.9 hours to the present 24 hours. Based on a comparison of the earths LOD and atmosphere – free temperature vs the moons, Id estimate this would have affected the earths surface temperature by only about 0.15 deg C. Would you agree? Not an important result, but in todays environment it is important to know what is not important.
pochas94,
The empirical observations show that rotation speed has no effect on the average surface temperature of a planet … See my reply to Roy above.
See my reply to your reply above. Radiation characteristics of the atmosphere are important.
Ned, I suspect you didn’t even read my post. The explanation of the “cold moon” is clearly the result of the long daytime elevating the surface temperature way up the S-B curve. Imagine solar illumination of an object that flickered between 0 and 1000 watts per square meter very rapidly…you could get the resulting temperature off the SB curve at 500 watts per square meter to high accuracy. Then imagine the solar illumination is 1000 watts for a hundred days, then 0 watts for a hundred days. Take those 2 points off the SB curve and average them together. The temperature difference for those different cases is huge. All that has changed is the length of the diurnal cycle!
Interesting post, Dr. Roy, thanks.
As you point out, postulating an earth with oceans but without an atmosphere is to juxtapose two “incompatible” notions.
In fact, you cannot logically postulate an earth with oceans but no atmosphere or GHE.
Likewise, the hypothetical earth with tropical oceans that freeze under insolation at solar zenith of 1360 W/sq m is another absurdity.
Interesting analysis of the limitations of the S-B equation in view of the variability of real world scenarios.
Ultimately irrelevant because the greenhouse effect is a result of conduction and convective overturning rather than downward radiation from a thin cold atmosphere to a hot dense surface.
And…we’re off to the races….
Not really, I’ll keep it very simple.
You must agree that conduction from air to surface is minimal due to the density differential so it must follow that radiation from air to surface is similarly limited by the ensity differential and that problem for the radiative theory is compounded by only a fraction of the atmosphere having radiative ability at all.
DWIR can’t do the job. Only the warming of descending air can achieve the observed effect. You have conceded that descending air warms have you not?
Dr. Spencer,
This is very interesting subject and analysis. One thing that I would like to add is that the Stephan-Boltzmann equation apples to land and does not apply to surface water. As a result, Earth’s surface temperature is “resilient” because of ocean, which has much larger thermal capacity than land.
Unlike land, surface water radiation is controlled by convection heat transfer of water at surface, which is constant. Therefore, ocean radiation is constant, which is observed. Please see Loeb et al. (2016). Land radiation on the other hand fluctuates considerably between day and night. While this is relevant for the moon, it is much less relevant for the earth because of ocean. This is my opinion, and I could be wrong.
Nabil, please… the S-B equation applies equally well to water as land. Both emit long wave radiation at emissivities over about 0.95. That there is more evaporative cooling by water is true, and much greater vertical heat diffusion as well…but those are TOTALLY SEPARATE ISSUES FROM THE S-B EQUATION.
Roy said:
“Secondly, the 33 deg. C number isnt really the greenhouse effect, anyway. Its more of a total atmosphere effect, the final result after atmospheric convection has cooled the surface substantially below the very high temperatures the greenhouse effect would cause in the case of pure radiative equilibrium (see Manabe and Strickler, 1964).”
I would question how upward atmospheric convection can cause net cooling of a surface when warming occurs in the descending leg of convective overturning.
Because the atmosphere undergoes a net radiative cooling to space. Subsidence warming can be viewed as convective heating, Stephen. Barring orographic effects, about the only way for air to sink is to be forced to by convective ascent. Statically stable air does not sink of its own accord. The whole convective overturning circulation thus transfers heat from the surface to the atmosphere. You really need to learn more about convection if you are going to persist in this, Stephen. It’s been going on too many years and at some point I will no longer be wasting my time.
Sadly, Roy, you are quite wrong about convective overturning.
The average surface pressure is about 1000 mb. All pressures above that involve air with a descending element and all pressures below that involve air with an ascending element. The split is 50/50. Wind flows between the high and low pressure cells to try to remove the differentials but those winds are not truly horizontal once contact with the surface is lost. Basic meteorology.
Whilst the atmosphere as a whole is in hydrostatic equilibrium no individual component ever is and apart from very brief local exceptions no individual parcel of air is ever statically stable.
Thus the thermal effect of the whole convective overturning circulation is net zero for the globe as a whole.
You and the AGW proponents are in error in assuming net cooling from surface to air as a result of convective overturning and that error has led you to try to balance the energy budget by proposing an unfeasibly large thermal effect from DWIR to offset that error.
In reality the air is too low in density and largely non radiative so it cannot possibly produce a strong enough DWIR flow to measurably offset the upward DWIR from the hot dense surface.
No doubt there is such an offset but it cannot be anywhere near the value of 33K or whatever the true figure is because the density of the surface is magnitudes greater than the density of the air above and the entire mass of the surface is fully radiative whereas only a tiny fraction of the air has radiative capability.
As for ‘wasting your time’ may I respectfully submit that you have failed to address the various strong points that I have made over the years.
As an example you never did deal with my query as to how you thought convective overturning could be prevented so as to lead to an isothermal atmosphere around a rough surfaced rotating sphere illuminated from a point source such as the sun which inevitably leads to density differentials in the horizontal plane as a result of uneven surface heating.Such density differentials inevitably result in convective overturning.
As long as convective overturning can develop you can never get an isothermal atmosphere due to the conversion of surface KE to convective available potential energy (CAPE in meteorology) as the rising air moves up along the lapse rate slope. And the reverse on descent.
“The average surface pressure is about 1000 mb. All pressures above that involve air with a descending element and all pressures below that involve air with an ascending element.”
Sorry, Stephen, but you will never find that made-up concept in any meteorology text or published research I am aware of.
As long as buoyancy is created at the Earth’s surface through solar heating and greenhouse effect destabilization, there is a net convective transfer of heat from the surface to atmosphere. Condensational heating is usually involved. The actual temperature rise occurs simultaneously in rising air currents and the sinking air that is forced to subside in response to the rising air. The entire circulation cell (including the horizontal flows which must connect them) is warmed as a result. But buoyancy created at the surface is indeed a necessary ingredient….as you imply, just air rising and sinking by itself would not cause convective heating.
This is basic atmospheric science, consistent with published research, textbooks, and equations put in weather forecast models that replicate nature very well.
I have already addressed ad nauseum the theoretical isothermal atmosphere in the absence of IR cooling by the atmosphere, and don’t want to go through the explanation yet again just so you can argue with me.
That concept IS in the text books. All low pressure cells (below about 1000mb) contain rising air and all high pressure cells (above about 1000mb) contain descending air.
It is the rising movement that pulls the surface pressure below average and the descending movement that pushes surface pressure above average.
Maybe I should be giving up on you.
Your isothermal explanation has never dealt with the questions I posed of it.
You now say:
“just air rising and sinking by itself would not cause convective heating”
But it must, because the rising and sinking requires energy and that energy must be located at the surface and in order to fuel the rising and sinking it cannot be radiated to space. Instead it is locked into the overturning cycle by conduction from surface to air.
Are you suggesting that rising and sinking can occur with no energy to drive it ?
I’ll leave it there having said enough here.
Areas of high and low pressure are caused by ascending and descending air. As air warms, it ascends leading to low pressure at the surface. As air cools, it descends leading to high pressure at the surface. This is illustrated in the diagram below.”
from here:
http://www.metoffice.gov.uk/learning/learn-about-the-weather/how-weather-works/highs-and-lows/pressure
You are partly misinterpreting that cartoon, and it is also partly incorrect. High and low pressure are caused by vertically integrated temperature effects, called hydrostatic balance. The deeper the layer of cold air, the higher surface pressure will be. The deeper the layer of warm air, the lower surface pressure will be. That doesn’t necessarily mean the low will be warm at the surface and the high cold at the surface….it depends also on what the vertical temperature structure is as well.
And the rising and sinking motion is not as simple as that cartoon shows, either…those in the cartoon would be barotropic weather systems (like a hurricane) that are vertically aligned…in the UK, and outside the tropics in general, pressure systems are almost always baroclinic…they tilt with height…and both highs and lows have regions of ascent and descent.
Roy W. Spencer, Ph. D. says: September 28, 2016 at 4:52 AM
“As long as buoyancy is created at the Earths surface through solar heating and greenhouse effect destabilization, there is a net convective transfer of heat from the surface to atmosphere. Condensational heating is usually involved. The actual temperature rise occurs simultaneously in rising air currents and the sinking air that is forced to subside in response to the rising air. The entire circulation cell (including the horizontal flows which must connect them) is warmed as a result. But buoyancy created at the surface is indeed a necessary ingredient.as you imply, just air rising and sinking by itself would not cause convective heating.”
Why is it that you neglect the obvious outward heat convection of the mechanically, not thermally induced Hadley and Polar cells? This mechanical convection provides 90% of the sensible and latent heat distribution in Earth’s atmosphere. This convection remains present even without the significant uneven insolation. So great is this convection vertical wind speed of 100 MPH at 3km altitude are noted near all longitudes near the ITCZ. It is this mechanically induced convection that results in the static low surface preasure near the ITCZ.
“Subsidence warming can be viewed as convective heating,”
Quite so.
So where does it appear in the energy budget?
It is contained in the ~100 W/m2 average convective heat flux from the surface to atmosphere. It is a necessary part of ALL rising air currents…they must be exactly matched by an equal mass of sinking air. The entire circulation cell experiences warming (except for the region where some of the cloud condensate that does not reach the ground as precipitation then re-evaporates into the air).
How do you get 100 W/m2 average convective heat flux upward (do you mean a radiative flux?) once the convective overturning cycle closes so that the kinetic energy taken up by rising air is then exactly matched by the kinetic energy returned to the surface in an equal mass of sinking air?
I think you are assuming that the additional warmth at the surface gives rise to an additional 100 W/m2 of upward radiation from the surface but that cannot be right because that extra warmth then just goes into the next conductively induced ascent.
You cannot have the same parcel of KE at the surface both radiating upward AND being absorbed by further conduction into the next overturning cycle simultaneously yet that is what you seem to be proposing.
Kinetic energy manifesting as heat is not itself radiation, it is vibrational movement.
Either a photon can be released OR the vibrations are passed on to adjoining molecules by conduction, not both simultaneously !!
To get the upward flux of 100 W/m2 there would have to be no contemporaneous conduction going on.
“The entire circulation cell experiences warming ”
No it does not.
It experiences the creation of convective available potential energy (not heat) at the expense of kinetic energy (heat).
Thus the adiabatic lapse rate slope which cannot be avoided in any system containing convective overturning.
Reversible in descent.
OMG, Stephen. Your use of the terminology and thinking is hopelessly muddled. I give up. -Roy
Roy,
There must be a simple logical assertion or fact that could show my thinking to be false if it as muddled as you say.
How does convection cause net surface cooling if, as you say, all rising air currents must be matched by an equal mass of sinking air and you accept that warming does occur within descending air as it moves down along the lapse rate slope?
Do you deny that adiabatic cooling is a fully reversible process?
Yes, adiabatic cooling is reversable…but that’s not relevant to the discussion.
If you heat the atmosphere from below through convective heat transport, the atmosphere will warm. The resulting rising air currents will be warmer than the ambient air (even while they are adiabatically cooling during ascent), and the sinking air currents (necessary for mass continuity) will also be warmer than the ambient air. There is then net convective heat transfer from surface to atmosphere.
The atmosphere, in turn, continuously radiatively cools to space. This is why the heat transfered from the surface to atmosphere cannot just be returned back to the surface, say from subsiding air. There must be a continuous net transfer of energy from warm surface to intermediate temperature atmosphere to the “cold” depths of outer space.
You have wrongly introduced radiation to space from within the atmosphere. That is a diabatic not an adiabatic process.
The adiabatic portion IS returned to the surface as heat recovered from CAPE.
Sinking air is NOT warmer than the ambient air until it picks up more conduction when it reaches the surface.
A descending high pressure cell is surrounded by rising low pressure cells which contain WARMER less dense air than the COLDER more dense descending air.
yes of course it is diabatic. Adiabatic means no energy gained or lost from an air parcel…well, hello!…that seldom happens in reality.
In reality the surface heats the air (diabatic), condensation drives moist convection (diabatic), radiation is continuously being gained and lost from air parcels (diabatic).
Weather processes, in general, are diabatic!!
I have no idea why you are so fixated on a theoretical concept (“a-diabatic”) that seldom occurs in the real world.
Again, you are throwing around technical terms, which is easy to do…but your thinking about how they work in the real world remains muddled, Stephen.
So now we have a complete denial of adiabatic processes within a convecting atmosphere.
All uplift and descent has an adiabatic component in so far as air is lifted up or lowered without adding or removing energy.
Density differentials in the horizontal plane caused by uneven surface heating cause just such uplift and descent all the time and everywhere.
No point commenting on that further having already referred you to a meteorology site that shows you are the muddled one.
Well, I don’t need you to agree with me (who has actually published on the causes of surface pressure, convective heating of the atmosphere, etc.) versus some graphic artist who might have had some cursory knowledge of some meteorological concepts. But I won’t have you spreading confusion and misinformation to others on my site about how weather works. Your comments are no longer welcome here. -Roy
Stephen Wilde says: September 28, 2016 at 5:16 AM
(“The entire circulation cell experiences warming )
“No it does not. It experiences the creation of convective available potential energy (not heat) at the expense of kinetic energy (heat).
Thus the adiabatic lapse rate slope which cannot be avoided in any system containing convective overturning. Reversible in descent.”
(OMG, Stephen. Your use of the terminology and thinking is hopelessly muddled. I give up. -Roy)
Stephen, Dr, Roy is correct Your terminology is lawyer talk! There is absolutely no gravitational potential energy in the troposphere. The increase in atmospheric temperature at lower altitude is part of the triplet of pressure, density, temperature increase near surface is induced and maintained by gravitational compression only it is a thermostatic condition. Not a thermodynamic process,which can be considered separately to modify the gravitationally induced condition. Any and all heat power/energy lifted outward is dissipated via EMR exitance to space. None returns to the surface. What you mistakenly call ‘warming’ on decent is but a return to the thermostatic KE in the form of air pressure. It is the compressive force field of Earth’s gravity that prevents the otherwise spontaneous surface gas expansion and any conductive heat transfer outward. This allows for all tropospheric mass relocation to remain isentropic (no work)!!
Roy, typo alert.
“The greenhouse effect is often claimed to cause an average warming of the Earth’s surface of about 33 deg. F….”
Should be 33 deg. C.
Cheers.
Oops.
Any thoughts on terra forming methods for Mars?
You can make oxygen from CO2. I looked into this after seeing the film “The Martian.”
https://en.wikipedia.org/wiki/Mars_Oxygen_ISRU_Experiment#Principle
Water once was plentiful. Now it has been absorbed into the crust. Need help from fracking plus in situ heating. Everything else is just bricks and mortar.
How much of the Earth’s temperature is due to GHE and how much the pressure effect?
On Venus, the high temperatures are almost entirely the pressure effect, because almost no sunlight reaches the surface. This is because of the highly reflective clouds of sulphuric acid.
There is no such thing as “the pressure effect”. The hydrostatic equation that tells how pressure and density vary with height does not constrain the temperature profile in any way. You can independently specify the temperature profile.
The fact that so little sunlight reaches the surface yet the temperature is so high is the result of the very large greenhouse effect.
Can somebody explain why rotation rate matters. It is said that radiation and conduction occur at equal rates in and out. The globe as much time for cooling as for warming. It seems logically that the rotation rate would not matter. The speed of rotation will establish a diurnal variation in daily temperatures but reaching an equilibrium in accordance with the inverse square distance law at 278.5k would result. It also seems for the same reason, cooling must contend with poorly radiating clouds equally both on incoming and outgoing.
I fail to see where the non-linearity of the Stefan Boltzman equations provide an avenue for the kind of variations being discussed.
It seems more practically that why a 33 degree greenhouse exists is because of the assumption that in order for the surface to produce radiation as a blackbody to fill the intial void in warming because of albedo the greenhouse effect must be that large. It must provide 23.5c to bring the surface up to equilibrium and the remainder 9.5 degrees is the “unique” greenhouse effect that raises temperatures above the expected.
So where am I going wrong?
I will repeat the simple example I provided above to answer your question:
Imagine solar illumination of an object that flickered between 0 and 1000 watts per square meter very rapidlyyou could get the resulting temperature off the SB curve at 500 watts per square meter to high accuracy. Then imagine the solar illumination is 1000 watts for a hundred days, then 0 watts for a hundred days. Take those 2 points off the SB curve and average them together. The temperature difference for those different cases is huge. All that has changed is the length of the diurnal cycle!
Roy,
you have the patience of a kindergarten teacher!
Roy Spencer says: September 27, 2016 at 5:25 PM
“I will repeat the simple example I provided above to answer your question:”
Thank you!
“Imagine solar illumination of an object that flickered between 0 and 1000 watts per square meter very rapidlyyou could get the resulting temperature off the SB curve at 500 watts per square meter to high accuracy.”
This is exactly the amplitude modulation that is attenuated by the thermal mass of Earth’s atmosphere as measured by physical in situ verification of physical thermal modulated EM flux at every frequency.
“Then imagine the solar illumination is 1000 watts for a hundred days, then 0 watts for a hundred days. Take those 2 points off the SB curve and average them together. The temperature difference for those different cases is huge. All that has changed is the length of the diurnal cycle!”
Indeed! The high frequency ‘modulation’ would have transferred attenuated sideband power into increased accumulated atmospheric sensible ‘heat’, especially evident in increase in mid tropical atmospheric temperature. Such did not happen!
This exemplifies the huge difference between the conceptual pseudo-scientific philosophical (‘is’) and this physical Earth! Which one do you wish to consider? The peons consider this earth’s physical. The Scienterrific else gets herded into the Volcano! Such must happen sooner or later! We have many hungry Volcanoes! Spontaneous EMR to space dispatches excess entropy! Volcanoes dispatch excess stupidity!
Will, are you on prescribed meds, or street drugs?
Roy W. Spencer, Ph. D. says: September 28, 2016 at 4:55 AM
“Will, are you on prescribed meds, or street drugs?”
Dr. Roy,
Did you participate in the field verification of the HiTran data base, or did I? I know what I was measuring, and it was not thermal radiative flux!
We’ve had a 56.7C surface temperature taken in El Azizia, Libya in 1913, and that’s with an atmosphere, and at 32.5N. But that’s the Horse Latitudes so there’s less atmospheric water vapour absorbing the incoming solar near infrared there. I don’t see what would stop a dry Earth with no atmosphere and average 0.1 surface albedo reach an equatorial midday temperature of around 383K.
“Secondly, the 33 deg. C number isnt really the greenhouse effect, anyway. Its more of a total atmosphere effect, the final result after atmospheric convection has cooled the surface substantially below the very high temperatures the greenhouse effect would cause in the case of pure radiative equilibrium (see Manabe and Strickler, 1964).”
Minus poleward heat transport, both oceanic and atmospheric. With an ocean world with an albedo of 0.06, the raw BB figure of 279K would be reduced to around 274.7 or 1.55C. So the current mean surface T is roughly a net 13C warmer than that, by whatever processes. How much of that is just heat redistribution to colder regions rather than greenhouse effect?
The funny thing is that it’s all that convection that puts the greenhouse effect up there 🙂
Ulric
“… its all that convection that puts the greenhouse effect up there”
Something which even climate specialists tend to overlook. Well explained here, I think: https://www.youtube.com/watch?v=slPMD5i5Phg
Dr. Roy,
This is your claim:
NOTE: Most of the comments on this post will likely be off-topic, centering around the extreme minority view of a few people that there is no atmospheric greenhouse effect involving the atmosphere emitting infrared radiation toward the surface.
You insist on some spontaneous thermal EM power flux (W/m²) in the direction of the higher temperature Earth surface from the lower temperature mass of Earth’s atmosphere. Have you any possible evidence of such physical thermal EM power flux?
All of the skilled engineering community agree that ‘exists’, an atmospheric thermal lapse rate involving higher Earth surface temperature than would be obtained by some childlike application of the established S-B equation. Many, many, alternate solutions involving atmospheric pressure, density, and radiative temperature effects, completely and scientifically explain such observation.
The only claim that is non scientific is yours of spontaneous ‘atmosphere emitting infrared radiation toward the surface’.
Roy relies on readings from pyregeometers for such evidence.
They are designed to sense the temperature of a remote solid object in the horizontal plane but Roy thinks it is valid to point them upwards to get the temperature of a non solid object such as the sky.
The sensor is triggered by an object more dense than the surrounding air so if you point it upwards to where there is no solid object it will be triggered at variable heights depending on the density of the air above. That density varies with cloud or particulate content.
If you point it up then it will be triggered at some variable point along the lapse rate slope and will record the temperature at that point but that is not an indication of DWIR flow, just the temperature at that particular height.
If the sky is clear the reading will be at a high cold location.
If the sky is cloudy the reading will be at a lower warmer location.
Roy thinks that the change in the reading when a cloud floats across is a result in a change in the DWIR flow but it isn’t. He is just recording the temperature at a different height along the lapse rate slope.
The sensor is able to record the temperature of a remote object by measuring the radiation coming from the object. Radiation is energy that will be absorbed by whatever it strikes, ie. DWIR.
The source of energy for the DWIR from clouds is water’s enormous latent heat of evaporation. CO2 never has enough energy to cause a measurable temperature change.
Stephen Wilde says:
“… [pyrgeometers] are designed to sense the temperature of a remote solid object in the horizontal plane…”.
Pyrgeometers are designed to measure near-surface infra-red radiation in the wavelength spectrum ~ 4.5 to 100 m. The fact that, when pointed skyward, pyrgeometers always detect radiation at such wavelengths indicates pretty conclusively that downwelling longwave radiation from the atmosphere to the surface is a physical reality.
TFN
It is a physical reality but it is cold, weak and in no way able to account for a surface temperature enhancement of 33K for the reasons I gave above.
You say “cold, weak” with your hand-waving explanation. But the measurements themselves disagree with you.
The measurements of DWIR intensity when put into a model (together with all other average energy fluxes) result in model-produced temperatures that match reality quite well.
All that you and others like you have is hand-waving generalities, Stephen.
Of course they match the reality quite well because you have substituted an assumed warming effect from DWIR in place of the missing warming from convective descent. You have (apparently arbitrarily) selected the warming effect of DWIR at a level that satisfies the requirement that the model outcome approximately matches reality.
Since, either way, the numbers are the same there will be a match with reality but the causation is wrong.
It is not hand waving to point out that an extremely thin density of gas of which only a tiny fraction has radiative characteristics cannot possibly play such a large part in the warming of a hot, dense, intensely radiative surface.
Nor is it handwaving to point out that there is nothing in the energy budget for any surface warming effect from convective descent. All I see is the incorrect assumption that the net effect of adiabatic convection is surface cooling at 100 W/m2.
It is for you to prove that the values allocated to the effect on surface temperature of DWIR are exactly right objectively and realistically.
Neither the model match with reality nor the output of pyregeometers achieves that.
Stephen,
‘It is not hand waving to point out that an extremely thin density of gas of which only a tiny fraction has radiative characteristics cannot possibly play such a large part in the warming of a hot, dense, intensely radiative surface’
I dont understand your point about density of gas. There are many situations where warm, low density gases produce tremendous radiation, e.g. neon light bulbs or for that matter all compact fluorescent light bulbs.
Nate,
The atmosphere is not composed of such gases.
Most of it doesn’t radiate at all and the components that do are miniscule with no comparison to neon or fluorescent light bulbs.
How can one get a whopping 33k out of it? How much brighter would the sun have to be to raise surface temperature by 33K?
Where is the empirical proof that it is from DWIR and not from the warming implicit in convective descent?
Nate says: September 28, 2016 at 8:56 AM
(Stephen,It is not hand waving to point out that an extremely thin density of gas of which only a tiny fraction has radiative characteristics cannot possibly play such a large part in the warming of a hot, dense, intensely radiative surface)
“I don’t understand your point about density of gas. There are many situations where warm, low density gases produce tremendous radiation, e.g. neon light bulbs or for that matter all compact fluorescent light bulbs.”
Nate, you are comparing electrically powered ionic discharge effects with EMR powered only by thermal(temperature) noise! The thermal noise is only a wee bit but has no OFF switch. OTOH Stephen again is but blowing smoke!
Rick says: September 28, 2016 at 1:59 AM
“The sensor is able to record the temperature of a remote object by measuring the radiation coming from the object. Radiation is energy that will be absorbed by whatever it strikes, ie. DWIR.
And such is scientific only because this is your fantasy? Your ‘radiation ‘ is just what in this physical world?
Are you saying that you don’t think that infrared radiation exists?
I only wish that you say what such physically is, (define) rather than claim some undefined fantasy!
“The measurements of DWIR intensity ”
There are no such measurements. All you have is measurements of the temperature at various heights in the vertical column.
Your pyregeometer simply measures the temperature at the height along the lapse rate slope where density triggers the sensor.
That does not represent a DWIR flux.
The only location where the radiative flux from the atmosphere is 33K higher than the S-B expectation is at the surface and that temperature is a result entirely of conduction and convection not radiation.
The radiation field is a consequence not a cause.
Stephen Wilde holds that “DWIR can’t do the job”. I think I understand him to think, mistakenly, that DWIR doesn’t occur? Or does he think that any DWIR is fully relected by the ground back into the atmosphere? Below Stephen writes:
As for wasting your time may I respectfully submit that you have failed to address the various strong points that I have made over the years.
I have watched this blog intermittently over some years. I think Dr Spencer is right to talk of Stephen wasting time, indeed all of our time, including Stephen’s own time.
It is hard to know how to respond to Stephen. He holds to a mistaken dogma, with obvious sincerity. It seems practically futile to try to reason with him on this topic. There are others who also hold the same or a like mistaken dogma, whereby he can draw comfort. It seems evident that he does not understand basic physical reasoning because he does not have a basic education in physics.
Meteorology is a more empirically based science than physics, in the sense that physics in many ways works on more rational lines. I do not mean that meteorology is irrational, nor that physics is not empirically based. I mean that the weighting between apodeictic theoretical reasoning and observational description is different between the two sciences. Stephen prefers the kind of descriptive presentation that is often useful in meteorology, as against the kind of apodeictic theoretical reasoning that is characteristic of physics. I think he doesn’t actually know or understand such physical reasoning. His remarks about pyrgeometers indicate that he sees them from a purely empirical viewpoint without understanding their theoretical basis. His idiosyncratic spelling “pyregeometer” may be indicative.
I think Stephen will only understand DWIR if he does some serious study of the physics of radiation. This will be difficult for him because he is not accustomed to the kind of thinking that is required.
Ok, I put an extra ‘e’ in pyrgeometer not having seen it often but I’ve seen worse versions.
As for theoretical physics being in some way ‘superior’ to the more empirical meteorology I think that is just hand waving.
If there is a logical flaw in my comments it should be possible to point it out simply enough for me to asses validity.
“If there is a logical flaw in my comments it should be possible to point it out simply enough for me to asses validity.”
But Stephen:
Can I put it this way.
Consider these 3 options….
a) All the world’s experts in thermodynamics going back ~150yrs to Tyndall & Arrhenius are wrong.
b) All the world’s experts in thermodynamics going back ~150yrs to Tyndall & Arrhenius are frauds.
c) They collectively know more than you.
I’m sorry – but why the correct one of those 3 points isn’t obvious to “Dragon-slayers” will remain a permanent mystery to me.
Absolutely!
Stephen,
‘Where is the empirical proof that it is from DWIR and not from the warming implicit in convective descent?’
You are the one making the extraordinary claims, akin to Toneb’s a) or b) above, that textbook atmospheric science is wrong.
Therefore doesn’t the burden of proof fall entirely on you, to show, quantitatively, that the conventional picture has a flaw, and that your alternative theory is the correct one?
Actually, Christopher is correct in his assessment of meteorologists versus physicists. That’s why my understanding of some important physical concepts (not well enough covered in even my PhD program in meteorology) has been greatly aided over the last 20 years by working closely with a PhD computational physicist.
Stephen Wilde writes:
As for theoretical physics being in some way superior to the more empirical meteorology I think that is just hand waving.
This is an example that shows the near futility of trying to reason with Stephen. He is missing my point, and responding to another of his own invention.
I did not write, nor do I think, that “theoretical physics is in some way ‘superior’ to the more empirical meteorology”. I wrote that the two sciences are differently weighted and that Stephen seems to lack understanding of characteristically physical thinking. Stephen would be right to make the point that my comment is not direct intrinsic engagement in argument in the topic. It is extrinsic comment on Stephen’s argumentative performance. Stephen calls it “handwaving”. ‘Handwaving’ in physics usually refers to loose talk that purports to be direct intrinsically engaged argument in the topic in hand, but is in fact no more than loose talk. So Stephen is not responding to my point. This is characteristic of his argumentation on this topic. I think it can be remedied only by his improving his understanding of basic physical reasoning, which is a steep slope for him to climb.
Stephen continues:
If there is a logical flaw in my comments it should be possible to point it out simply enough for me to asses validity.
For the reason I stated just above, Stephen’s comments are not tightly enough formulated to make it feasible to define their logical weakness simply enough for him to grasp. For that, he needs to climb that steep slope.
‘Your pyregeometer simply measures the temperature at the height along the lapse rate slope where density triggers the sensor’
But how does it measure temperature? It doesnt reach out and touch the air way up high. It does so by measuring IR intensity and calculating temperature from that.
Thus the measured temperature DOES represent a DWIR flux.
It measures the temperature at a specific height along the lapse rate slope.
If it then measures at a different height along that slope then the temperature will be different.
Which temperature represents a DWIR flux towards the sensor if either ?
The answer is that both could do so since the sensor will be triggered at whatever height has high enough density to be mistaken for a remote object. The DWIR flux recorded by the sensor therefore depends on atmospheric density. The higher the density the lower and warmer the height from which the flux appears to come.
But the air is magnitudes less dense than the surface and only a tiny fraction of it is radiative so how does one get enough DWIR from the air to raise the surface temperature by a whopping 33K?
The air is far too thin to conduct significantly to the surface so it is also far too thin to radiate significantly to the surface.
Proof please, without relying on models or pyrgeometers, of the actual thermal effect of DWIR on surface temperature.
Stephen
https://geosciencebigpicture.files.wordpress.com/2016/03/all-up.png
“But the air is magnitudes less dense than the surface and only a tiny fraction of it is radiative so how does one get enough DWIR from the air to raise the surface temperature by a whopping 33K?
The air is far too thin to conduct significantly to the surface so it is also far too thin to radiate significantly to the surface.”
No, you’re comparing conduction to radiation there. Apples and pears.
Stephen consider the Beer-Lambert Law
With particular regard to the path-length term:
Conceptually:
You have a powerful flashlight.
On a night of thick fog you shine it into it. Send a friend away into the distance and I’m sure you’ll agree that he/she will get to a point not to far away when the flashlight beam cannot be seen.
On a night of mist, you again shine your flashlight into it. Your friend again goes off but has to travel much further before the beam is extinguished.
Why does this not invalidate the GHE?
The mist simulates a low concentration of radiating molecules, BUT will still have a very sig effect on the transparency of the atmosphere to LWIR due to the long path-length to space.
Considering an average tropopause of (say) ~40,000ft/8 miles (and that’s just the vertical direction – most radiation will travel obliquely to that), then there is plenty of opportunity for photons to be intercepted and back-radiated.
Toneb,
The problem I see with that is the decline in temperature with height so that the higher one goes the colder the temperature and the weaker IR emission becomes even before any interception or back scattering.
I need to see proof that DWIR rather than descending convective warming causes the surface temperature enhancement or maybe a division between the two potential causes.
You see it isn’t radiative loss to space that causes the lapse rate slope. Instead it is the decline in density with height which points to conduction and convection being the cause rather than radiation.
The point being that if one involves atmospheric mass in the GHE phenomenon then any radiative component fades into insignificance.
Stephen,
Just to be clear, you don’t deny that ultimately it is radiation to space that balances the incoming solar?
Further, you dont deny that the upper atmosphere radiates to space? Do you?
“You see it isnt radiative loss to space that causes the lapse rate slope. Instead it is the decline in density with height which points to conduction and convection being the cause rather than radiation”
Stephen:
Yes, the LR is caused by atmospheric motion and in the relation -g/Cp.
The GHE is not significantly involved except locally where effects can be visible but they are generally smoothed away by motion quite soon.
Again – the GHE does NOT cause the LR we see, which is modified locally in a myriad ways as per air-mass characteristics and subsidence, evaporative cooling etc.
It is perhaps a mistake that I am about to try to reason with Stephen Wilde. He writes:
You see it isnt radiative loss to space that causes the lapse rate slope. Instead it is the decline in density with height which points to conduction and convection being the cause rather than radiation.
There are many flaws in these two sentences.
(1) to speak of what “causes the lapse rate slope” is poor expression (tightly criticized, it is poor metaphysics). Stephen wants to know the explanation of the lapse rate. Usually in tight reasoning, it is localized and temporary events or transient processes that are caused. Roughly speaking, the lapse rate, as referred to by Stephen, is an approximately steady state. Steady states have explanations, not causes in the usual sense.
(2) Stephen is here appealing to his dogma that decline in density fully explains the lapse rate. He is not, in these two sentences, presenting an argument for his dogma.
(3) Stephen’s two sentences seek to hide the importance of radiation from the atmosphere to space. Radiation from the ground penetrates clear through the atmosphere to an extent of, in round numbers, 60 W m^-2. The remaining radiation to space from the earth is from its atmosphere. Most of that is from the troposphere. In round numbers let us say 180 W m^-2. Total radiation to space (round numbers) 240 W m^-2. The radiation from the ground absorbed by the atmosphere is about (round numbers) 330 W m^-2. The total radiation from the ground is about (round numbers) 390 W m^-2. This makes the optical depth of the atmosphere at relevant wavelengths about ln (390/60) = 1.87. Non-radiative (evaporation, conduction) transfer from the ground is about (round numbers) 100 W m^-2.
Sorry, I hit the ‘submit’ button by mistake before I was ready. Please disregard the immediately foregoing post of September 29, 2016 at 5.11 am. I will try to post a finished version when I am ready.
It is perhaps a mistake that I am about to try to reason with Stephen Wilde. He writes:
You see it isnt radiative loss to space that causes the lapse rate slope. Instead it is the decline in density with height which points to conduction and convection being the cause rather than radiation.
There are many flaws in these two sentences.
(1) to speak of what causes the lapse rate slope is poor expression (tightly criticized, it is poor metaphysics). Stephen wants to know the explanation of the lapse rate. Usually in tight reasoning, it is localized and temporary events or transient processes that are caused. Roughly speaking, the lapse rate, as referred to by Stephen, is an approximately steady state. Steady states have explanations, not causes in the usual sense.
(2) Stephen is here appealing to his dogma that decline in density fully explains the lapse rate. He is not, in these two sentences, presenting an argument for his dogma.
(3) Stephens two sentences seek to hide the importance of radiation from the atmosphere to space. Radiation from the ground penetrates clear through the atmosphere to an extent of, in round numbers, 60 W m^-2. The remaining radiation to space from the earth is from its atmosphere. Most of that is from the troposphere. In round numbers let us say 180 W m^-2. Total radiation to space (round numbers) 240 W m^-2. The radiation from the ground absorbed by the atmosphere is about (round numbers) 330 W m^-2. The total radiation from the ground is about (round numbers) 390 W m^-2. This makes the optical depth of the atmosphere at relevant IR wavelengths about ln (390/60) = 1.87. Non-radiative (evaporation, conduction) transfer from the ground is about (round numbers) 90 W m^-2. Solar light absorbed by the atmosphere is about (round numbers) 80 W m^-2. Solar light absorbed by the ground is about (round numbers) 160 W m^-2.
Upwelling radiation from the layers of atmosphere near the ground is significantly absorbed on its way by the troposphere, and only partly escapes clear to space. Upwelling radiation from the upper troposphere has a relatively clear path to space. Contrary to Stephen’s dogma, downwelling radiation from the layers of atmosphere near the ground is significantly absorbed by the ground. A lesser amount of downwelling radiation from the upper troposphere will make it to be absorbed by the ground, the rest being absorbed by the lower atmosphere. If there were only radiative energy transfer, as just described, the lapse rate would be greater than it is. Non-radiative transfer, nearly all convective, reduces that background notional purely radiative lapse rate to its actual value. Such convective transfer may then be said to govern the lapse rate, but it is an action to counter the larger notional radiative lapse rate. Thus both radiation and convection are important in determining the lapse rate. Neither alone does it.
The convection is by approximately adiabatic transfer. That is why the lapse rate is described as adiabatic. Adiabatic convective transfer is a more or less continual process in the troposphere. It transfers a continual flux of energy from the bottom of the atmosphere upwards within the troposphere. This supplies energy for radiation to space clear from the troposphere.
The troposphere is thus at all times far from thermodynamic equilibrium. Thermodynamic equilibrium is defined by the permanent vanishing of all flows. It is thus a mistake to accept the entropy-maximizing account of the lapse rate proposed by Bohren & Albrecht. Entropy maximization is for thermodynamic equilibrium. For non-equilibrium scenarios, ordinary thermodynamic entropy is not defined. The use of ordinary thermodynamics for atmospheric calculations is an approximation that makes sense only in special circumstances. It does not provide full explanations of atmospheric physics.
I suppose Stephen will feel that the above account unjustly assumes what is intended to be demonstrated. I can suggest only a careful study of radiative transfer in gases as a remedy for such a feeling. There are several reliable texts on the topic. One is by R.M. Goody and Y.L. Yung, Atmospheric Radiation: Theoretical Basis, second edition, Oxford University Press, 1989.
Christopher, I have banned Stephen from posting any more comments here, so he won’t be able to respond (unless, like D0u9 C0++0n, he pretends to be someone else). -Roy
In all that, I forgot to deliver the punch line.
Downwelling radiation from the atmosphere absorbed by the ground is about 320 W m^-2.
C. Game,
Latent energy emission at the surface = 80 W/m^2; this is about 50% of insolation at 160 W/m^2. DWLWIT absorbed by the surface = 320 W; latent heat emission = ZERO.
How does this line of reasoning square with apodictic physics? Because the surface of the ocean cools primarily through evaporation, unless studies concerning this are mistaken.
What is particularly impressive about Stephen Wilde’s “theory” that descending air warms the surface is that he manages to violate the Second Law of Thermodynamics (having net convective heat transfer be from the colder atmosphere to the surface) and still doesn’t explain what he is trying to explain.
No amount of transfer of energy from the atmosphere to the surface can help remedy the fact that the surface is at a temperature where it would be impossible for the energy balance to be satisfied at the TOP OF THE ATMOSPHERE without having greenhouse elements (gases and clouds) absorbing some of the radiation that is emitted by the surface. Stephen can not be made to understand that it is not the energy balance between the surface and the atmosphere that he has to explain but the balance between the Earth + atmosphere and the rest of the Universe. [When this is pointed out to him, he inevitably tries to get out of it by proposing to change the known physical laws. For example, he claims that a surface that is also transferring heat by conduction is then not radiating the amount that the laws of physics say it radiates.]
Furthermore, we know what the solution to the conundrum of the surface emitting too much radiation is because we have spectral data from satellites showing how that radiation gets absorbed by the greenhouse elements of the atmosphere in precisely the way predicted by radiative transfer theory.
So, Stephen’s “theory” fails on 3 accounts:
(1) It violates a bedrock foundational law of physics (the Second Law of Thermodynamics).
(2) It still doesn’t explain the Earth’s surface temperature even if you allow for this violation.
(3) It is contradicted by experimental data…Or, more precisely, the experimental data are in excellent agreement with the conventional theory and physics.
It is hard to see how you can do much worse than that!
mpainter, thank for your comment. It is rather telegraphically expressed and I am not sure what you mean. Please expand a little to clarify it for me.
Christopher Game says: September 29, 2016 at 6:34 AM
In all that, I forgot to deliver the punch line.
“Downwelling radiation from the atmosphere absorbed by the ground is about 320 W m^-2.”
“Downwelling radiation”, is but a conceptual Climate Clown political SCAM, with no science at all! Never ever any physical science meaning offered. Just accept cause mommy said so! And shut up and eat your peas! This amounts to all of C. Game science.
An instrument with upward field of regard measures upward thermal EM radiant exitance in W/m² of its thermophile in the 3-9 micron band. This exitance to space is nowhere near the 340 W/m² exitance to space as claimed by C. Game as “upwelling radiation” from the surface!. Even on a cold clear night that measured upward exitance is no more than 3 W/m² or 1% of such dastardly claim.
Even this wee amount is strictly limited by any local atmospheric water, in any phase, creating its opposing field strength (‘radiance’) in that 3-9 micron band, that C. Game calls ‘downwelling radiation’, shut up and eat your peas, no backtalk, or else! C. Game has never bothered to learn or use any proper radiometric terms of science.
YOU HAVE BEEN GAMED! As in, Gaming the system (also referred to as gaming the rules, bending the rules, abusing the system, cheating the system, milking the system, playing the system, or working the system) Do you feel better now?
Christopher Game:
Has to do with partitioning of the energy loss at the surface: latent, radiation, or sensible. The energy budget diagrams show all back radiation “absorbed by the surface” as returned without partitioning, that is, as IR. This partitions surface energy emissions as latent energy loss at ~15%, radiant energy loss at > 80%. This is a glaring discrepancy with partitioning studies that put latent at 60% and radiative at 30%. Do you see the problem?
Thank you, mpainter, for this extra detail. The round numbers I offered fit two balances for a steady state: conservation of energy in the ground, and conservation of energy in the atmosphere. For each, the sum of absorbed fluxes equals the sum of emitted fluxes. I think I have the arithmetic right. For each mode of transfer, there is a distinction between the total energy transfer and the two one-way fluxes that comprise it. Your comment does not tell me exactly how you think about that.
Christopher, you avoid the issue that I raised.
I don’t understand the issue you claim to have raised. The net IR flux at the surface is a net loss, which is about 35% of the total rate of energy loss (convective loss is about 65%), and I think Christopher would agree with that. So what is the point you are making? -Roy
Roy, by “surface”, I mean precisely that: air/water interface. Partition of energy loss at the sea surface, according to one study: latent = 60%; radiative (IR) = 30%; sensible = 10 %. How can this partition scheme be reconciled with the energy budget diagrams which show 330 W/m^2 back radiation “absorbed at the surface” yet emitted to the atmosphere as IR, unpartitioned?
To put it another way, total radiant energy absorbed by the surface (insolation + back radiation) = 490 W/m^2. Energy budget diagrams show ~80 W/m^2 of this is emitted as latent energy. This = ~15% of the surface energy emissions as calculated per energy budget diagrams.
Is the partition of latent energy loss at the sea surface correctly given at 60%? Or is the correct figure 15%?
So far, no one has addressed this problem, although I have raised it numerous times.
Essentially it is a question of how the back radiation “absorbed by the surface” is properly partitioned in the surface energy emissions.
I hope that I have managed to present the issue clearly.
Nature doesn’t think in terms of “partitions”…there are energy fluxes, and we group them in ways that we find meaningful for discussing them. You seem to want to group them differently, and then talk about relative sizes of them in your new method…fine. But it doesn’t change the individual energy flow rates, and the sum of energy gains versus losses is still zero (or close to zero, if you believe there is a current very small radiative imbalance in the climate system). -Roy
Dear Will Janoschka, judging from your comment of September 30, 2016 at 12.53 am, I think you ridicule my thoughts. I guess that means you wouldn’t be interested in discussing the topic with me. If you would be interested, may I suggest you post again.
Christopher, I have reached my limit with Will and his condescension, and have banned him. -Roy
Thank you, mpainter, for your comment. No, I am not trying to avoid your point, I am trying to get it clear in my mind before replying to it.
Working with the round numbers that I proposed above (September 29, 2016 at 6.31am:
Radiation at the ground:
emitted total: 390 W m^-2
absorbed total: 320 W m^-2
net loss: 70 W m^-2
Non-radiative at the ground (sensible + latent = conductive + evaporative)
net n-r loss: 90 W m^-2.
Total loss from ground:
(70 + 90) W m^-2 = 160 W m^-2
Percentage by
non-radiation: 100 90/160 % = 56%
radiation: 100 70/160 % = 44%
Dr Spencer gives 65% and 35%.
mpainter’s study gives:
latent: 60%
sensible: 10%
total non-rad.: 70%
radiative: 30%
I wouldn’t quibble over these numbers. I think this is near enough agreement for the present topic.
Of the total radiative loss from the ground by my round numbers:
escapes
clear to space: 60 W m-^2
retained
by atmosphere: 100 W m^-2.
The figure I use, 60 W m^-2, would be regarded as too big by many. Perhaps they may be right.
On my round numbers, the energy gained by the ground by radiation is:
solar radiation: 160 W m^-2
back radiation: 320 W m^-2
total radiation: 480 W m^-2.
On my round numbers, the energy emitted by the ground is:
Planck radiation: 390 W m^-2
non-radiative: 90 W m^-2
total: 480 W m^-2.
As for the questioned figure 15%:
Suppose the non-radiative loss is split:
sensible: 10 W m^-2
latent: 80 W m^-2.
Then 100 80/480 % = 17%
Near enough agreement for me.
Christopher, thanks for your response.
Using your figure of 17%, I see no agreement between that and 60%. The issue is this: which figure gives a reliable partition of latent energy emission at the sea surface? In the answer to this question are important implications for energy budget diagrams.
‘Partition of energy loss at the sea surface, according to one study: latent = 60%; radiative (IR) = 30%; sensible = 10 %.’
If we interpret ‘energy loss’ to be NET IR + non-radiative then there is no disagreement.
At sea/air interface you put a net IR emission? Nonsense.
Why nonsense? You yourself say 30% of loss radiative.
Fine, Nate. Show me your calculations for a net UWIR at the sea/air interface. Please give the gross figure and the amount deducted from the gross to achieve your net. At the interface. Please and thank you.
It’s confusing to use terms like “gross figure” and “net UWIR”. There is instead 1) UWIR and 2) DWIR. Their sum (assuming they have opposite signs) is the net IR. What part of this do you have a problem with? -Roy
Ok, To repeat what Christopher Game stated:
390 UW
320 DW
net 70
If you know better numbers for sea surface from your ‘one study’ source, then please tell us what those are.
Thanks for your calculation, Nate.
As I suspected, you wind up with the 165 W/m^2 of insolation: 80 W (latent energy) + 70 W IR + 15 W sensible heat.
Thus you demonstrate mathematically that back radiation adds no energy to the surface. But the energy budget diagrams show otherwise. Big problem for AGW mathematics.
Christopher, presumably you endorse Nate’s math.
mpainter, the two figures differ in their denominators, with one and the same numerator. They are both reliable. The 60% has as its denominator the total of the net (two-way) losses from the ground. The 17% has as its denominator the total of the one-way emissive fluxes from the ground.
‘you demonstrate mathematically that back radiation adds no energy to the surface.’
No, don’t get your logic here.
The math shows it adds 320. This achieves near balance.
Without the 320 the surface would (all else being equal) radiate a net 390. And would cool rapidly.
See Roy, I’ll say precisely what I do not understand. The energy budget diagrams are explicit: “330 W/m^2 absorbed at the surface”. This explicitly adds to insolation. But it is not accounted for in surface energy emissions. Only insolation is. It defies logic.
Regarding your claim that partition of surface energy emissions is unnatural, I consider that a doubtful statement. Certainly those who conduct such studies would not agree with your views.
So, 330 W of back radiation “absorbed by the surface” is to be disregarded and only the 165 W of insolation is accountable in surface energy emissions. As per Nate’s math. Incomprehensible.
Also, back radiation is absorbed at the interface or within a few microns. This energy is transient, being returned to the atmosphere within a few seconds as latent heat or as radiation, or sensible heat. Partition that, and you get 17% as latent energy, according to AGW calculation. According to partition studies, it should be 60%. Who lacks understanding? Those who write partition studies?
‘330 W of back radiation absorbed by the surface is to be disregarded and only the 165 W of insolation is accountable’
Nobody is disregarding it. Nobody is counting only insolation.
Without the back radiation, there is no energy balance.
to be very clear, add it all up: downward is +
insolation +165
dwir +320
uwir -390
non-radiative -95
sum = 0
cant disregard any of these terms.
But partition studies put surface IR emission at 30%. Not 80%. Are these studies incorrect? I don’t think so. Your 390 W of radiation by the surface is not in accordance with these.
Once again, back radiation is explicitly added to insolation by the energy budget diagrams. There is the basis for partition of surface energy emissions. Your math returns back radiation to the atmosphere as IR. This is the perpetual motion notion.
‘Your 390 W of radiation by the surface is not in accordance with these’
390W is just SB of room-temp dark ocean
‘Once again, back radiation is explicitly added to insolation by the energy budget diagrams’
Please find the flaw in the math I showed.
‘Your math returns back radiation to the atmosphere as IR. This is the perpetual motion notion.’
If the surface is warm it radiates by SB, no more no less. No perpetual motion
The flaw is in the assumptions behind the math, as I pointed out. This seems to elude you. Enough. Partition the DWLWIR incident on the sea surface and you will be partitioning the kinetic energy in the uppermost five microns as it is radiated/conducted/evaporated to the atmosphere.
And no, it doesn’t “radiate according to SB”. What does SB have to do with evaporative cooling? You studiously ignore partitioning of surface energy emissions.
mpainter, till now I haven’t seen you respond to my post of September 30, 2016 at 1:49 PM.
Your comment needs elucidating, if you want me to respond, thanks.
First you wanted to discuss in terms of math, which is best because it is precise:
‘Show me calculations..”
I showed them, but then you turned the math back into words that are imprecise:
‘Thus you demonstrate mathematically that back radiation adds no energy to the surface.’ you said some terms are ‘disregarded” and not all are “accountable”
I then carefully showed you math that proved these statements are incorrect. The various fluxes sum to 0. All fluxes including back radiation are essential and must be counted to achieve this.
But you again turn straightforward math into imprecise words:
“Partition the DWLWIR incident on the sea surface and you will be partitioning the kinetic energy in the uppermost five microns as it is”
I don’t understand what this means? Please stick to math whenever possible. Address the terms that are summed and explain how they are wrong if you think they are wrong.
As you did here: Your 390 W of radiation by the surface is not in accordance with these
And I’ll repeat my answer, the 390W is SB–near black-body radiation. You can quibble slightly with the number but this radiation must be there!
As you say “What does SB have to do with evaporative cooling?”
Nothing to do with it. They are both going on independently. We already included evaporative cooling in the term ‘non radiative’ -95W
mpainter, my post I that haven’t seen your response to reads:
mpainter, the two figures differ in their denominators, with one and the same numerator. They are both reliable. The 60% has as its denominator the total of the net (two-way) losses from the ground. The 17% has as its denominator the total of the one-way emissive fluxes from the ground.
Yes, Christopher, that is what need elucidation.
Nate, I conclude that you are incapable of addressing the physics of the sea surface. You deceive yourself with your doctrinaire formulations. The back radiation is absorbed at the interface or within a few microns and the absorbed energy is emitted to the atmosphere within seconds. Your problem is to partition that emission. That is the physics of DWLWIR. But it seems to elude you.
Mpainter, I doubt you will find any oceanographer who believes that ~300 W/m2 of DWIR immediately goes into evaporation…especially when the average evaporation from the ocean surface is only about 100 W/m2! If you are claiming that only departures from the average go immediately into evaporation, how does that work? How does the sea surface know which Joule of energy is part of the average, and which isn’t? I don’t know where you pick these ideas up from. -Roy
Also Nate, SB does not apply to transparent surfaces that cool evaporatively. There is no radiative equilibrium at the sea surface. You fail to grasp even the basics, I’m afraid.
“SB does not apply to transparent surfaces that cool evaporatively”?? Where does THAT come from?? I’m sorry, Mpainter, but I’ve grown weary of the made-up physics you try to infect others with here. Go do it elsewhere. -Roy
mpainter, you ask:
Using your figure of 17%, I see no agreement between that and 60%. The issue is this: which figure gives a reliable partition of latent energy emission at the sea surface? In the answer to this question are important implications for energy budget diagrams.
The percentages are ratios with numerators and denominators, multiplied by 100.
They have the same numerator, the latent heat transfer from ground (or sea) to atmosphere, say (my round number) 80 W m^-2.
My figure of 17% has the denominator 480 W m^-2, the total one way flux from the ground (or sea).
The figure of 60% has the denominator (my round number) 160 W m^-2, the total two-way loss from the ground, radiative 70 W m^-2 + non-radiative 90 W m^-2.
Both ratios are reliable. They have different denominators. It is a matter of choice which of them (if either) one finds interesting or enlightening.
mpainter,
I tried. I tried to have a fact-based logic-based math-based discussion with you.
And I tried to be patient and go through with you step by step. But all to no avail.
In the end you never acknowledge points of agreement, and you always return to word salad (partition, etc) or made-up physics (‘SB does not apply to transparent surfaces that cool evaporatively’), in order to preserve your prior beliefs.
There is just no point in continuing.
Unfortunately, I have had to ban mpainter from further comments. I refuse to have him infecting minds with pseudo scientific silliness.
My just foregoing “total two-way loss from the ground (160 W m^-2)” stands against (does not include) and balances the solar light absorbed by the ground (160 W m^-2).
Hi Roy,
It seemed that mpainter and Christopher Game were having a reasonable non-offensive discussion (not that I understood everything).
Earlier in the blog mpainter even stated:
“Interesting post, Dr. Roy, thanks.”
It’s your blog, but IMH opinion, banning mpainter was a little harsh, for what its worth.
It wasn’t for being insulting. It was for pushing nonsense as science. As I said, I won’t have my blog used to infect people with falsehoods. I can’t always monitor what’s said, but I can keep people who repeatedly push fake science from peddling their ideas here. They can do it someplace else.
Ozone radiates in the infrared. So why the average temperature of 0.1 bar is always the lowest?
http://www.cpc.ncep.noaa.gov/products/stratosphere/strat-trop/gif_files/time_pres_TEMP_MEAN_ALL_EQ_2015.png
Why probe shows that the lowest temperature on Venus is at a pressure of about 0.1 bar?
http://www.datasync.com/~rsf1/vel/1918-3b.gif
http://www.datasync.com/~rsf1/vel/1918-4a.gif
Dr Roy, just wondering, is this a submitted paper?
Nope. Just a simple calculation done in response to a claim that the Moon’s temperature can approximate what the Earth’s temperature would be like without an atmosphere.
What about the Diviner lunar temperature data?
http://onlinelibrary.wiley.com/doi/10.1029/2011JE003987/full
yes, that’s some of the data I compared my simple model to.
“[53] It is clear from the Diviner EDS data that the assumption of isotropic emission is incorrect. Noon surface temperatures measured near 8 μm are greater than radiative equilibrium temperatures, even if one assumes that A = 0. At the closest Moon-Sun distance, maximum temperatures of 397.5 K and 390 K are predicted for A = 0 and A = 0.07 (mare), respectively, while the warmest measured brightness temperatures reach 399 K.”
sounds pretty close to me, considering potential calibration problems with a satellite-borne IR radiometer.
That is much warmer than your model, and late afternoon-dusk on your model has a rather too soft knee compared to observations, both suggest that you have too much dampening in the model.
Not surprising. My simple model (which took me less than 2 hrs to produce) uses a simple, single bulk heat capacity for the soil. To get a more accurate diurnal cycle in surface temperature, you would need to have a multi-layer surface model that includes depth-dependent thermal conductivity and heat capacity profiles, which vary strongly with depth on the Moon.
In order for Roys’ theory to be true then an experiment is required. Shine IR at a rotating sphere and measure the temperature for different rates of rotation. Common sense would say that the temperature was independent of the rate of rotation since the sphere absorbs as a circular cross section.
I have just thaugt of an Earth with no GHG’s. You can split it in two parts, the tropics from 30 to -30 and the rest.
The tropics receive in average 1/3 of 1365W/m2 = 455W/m2 and the rest receives in average 1/6 of 1365W/m2 = 228W.
It equals respective 25C and -22C.
Wonder what kind of wind it could make in an radiative inactive atmosphere?
From the other thread now closed by SKYintest Spencer
Norman says: September 29, 2016 at 12:26 PM
Will Janoschka
Up above you write this: Interesting All of your BS refers to thermal EM flux after generation and that flux must do such! Not even one word as to how, why such flux is ever produced. Not even one word!!! The radiant terms intensity, radiant intensity, radiance, spectral radiance, specific intensity! all that deal with how, why, and how much, flux may possibly be expressed/generated. Is your intention truly to SCAM all rather than enlighten any?
This link will give you all the answers you ask for in extreme detail. Please read it to update your knowledge levels of EMR.
http://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Spectroscopy/Vibrational_Spectroscopy/Infrared_Spectroscopy/Infrared%3A_Theory
Norman troll I asked for nothing except your learned pointing out of any technical/scientific mistakes I might have made in my current posts. I make many! Always have, always will! Some others can identify such, from which I learn from my mistakes! I reject your incessant insistence that this true physical is recorded in documents that I helped write!
Will Janoschka
Well you did not help write the link I posted.
References
D. A. Skoog, F. J. Holler, S. R. Crouch. Principles of Instrumental Analysis, 6th ed. Belmont, CA. Thomson Higher Education. 2007
G. D. Christain. Analytical Chemistry, 5th ed. New York. John Wiley & Sons, INC. 1994
R. S. Drago. Physical Methods, 2nd ed. Mexico.Saunders College Publishing.1992
S.M. Blinder. Introduction to Quantum Mechanics. Academic Press. 2004
D. C. Harris, M. D. Bertolucci. Symmetry and Spectroscopy: An Introduction to Vibrational and Electronic Spectroscopy. New York. Dover Publications, INC
Contributors
Richard Osibanjo, Rachael Curtis, Zijuan Lai
zo fI do not see any Will Janoschka listed anywhere in the references or the contributors.
Did you at least read through the material?
Test. of Spencers stuff http://joannenova.com.au/2016/09/weekend-unthreaded-135/#comment-1842198
I now learn that you Norman, are indeed not a SKS John Cooook autobot!You now appear as a Dr. Roy creation still requiring peer review, plus proper citation of everybody!
Dr. Roy, Can you not afford a proper programmer for your site, that gives a wee bit of technical/scientific credibility?
Will Janoschka
Believe what you want about me, it is most certainly wrong as are most the science in your posts.
Your recipe:
1) Add a cup of technical jargon that sounds like you are highly intelligent (note the “sounds” part since you have no clue what the terms mean that you post).
2) Add the names of a few famous scientists to impress the scientifically illiterate. (Whoa, Maxwell, that means Will must be a genius and I need to listen to all the things he writes)
3) Mix well and splatter in incoherent fashion (which again my fool the scientific illiterate but no person with any science background would consider your posts valid on any point you make)
4) Add a few paranoid conspiracy ideas (Norman does not accept my ridiculous posts as valid therefore it is a conspiracy, he is a program created by Dr. Roy to discredit my brilliance)
5) Make sure to take the mixture out of the oven after just a half cooking to make sure the post is “Half-baked”.
6) Pat self on back for a brilliance not shown in any post but it sounded good to you when you typed it in.
Uh oh. Looks like my AI program called “Norman” has become self-aware now. Watch out, Skynet.
Roy W. Spencer, Ph. D. says: September 30, 2016 at 8:08 AM
“Uh oh. Looks like my AI program called Norman has become self-aware now. Watch out, Skynet.”
Whoo, whoo! Can you Dr. Roy or ‘Norman’ post any creditable scientific error to any that I have tried to explain as some, any, alternate to your political SCAM? I indicate no conspiracy only abject stupidity and glutinous feeding at the public trough!
“Abject stupidity”? Congratulations, Will, you have just joined the small but elite class of banned commenters here. -Roy
What I do not at all understand is how people can doubt about downwelling IR, although there is scientific evidence about it due to a long experiment spaning over 10 years:
http://newscenter.lbl.gov/2015/02/25/co2-greenhouse-effect-increase/
Even if I wouldn’t accept this be due to CO2: at least I would feel obliged to accept that DWIR is a fact…
“Even if I wouldnt accept this be due to CO2: at least I would feel obliged to accept that DWIR is a fact”
From what I’ve experienced when posting that link is that of the like …. “Just 2 places on Earth” and “the forcing is computed from a model”, and there is no evidence that has increased temps.
They gloss over the observation of increasing down-welling LWIR increasing as CO2 increases as soon as a model is introduced and also exercise the impossible expectations of 100% certitude.
Roy, your calculation is still wrong, as is Willis E’s, as is N&Z’s.
Standard radiative physics gives exactly the right value for the average, for the peak value, and for the shape of the temperature curve as well. On a body like the moon, with essentially no atmosphere, there is no large scale equilibrium, so the temperature at any point on the dayside is due to its radiation at that point.
As I showed in this calculation, this gives exactly the right answer for the average equatorial temperature, the peak value, and the right shape of the temperature curve.
http://davidappell.blogspot.com/2012/04/norfolk-constabulary-made-wrong-charges.html
I think we are closer in agreement than you imply, David. I suggest you try the calculation over the full diurnal cycle, at different latitudes, and do your own area average. What do you get? My only point was that for the moon, with its slow rotation and with no atmosphere, you cannot compute the global average temperature from the global average absorbed solar flux. Try it and see what you get. Nikolov was right about this, and I try to give credit where credit is due. What’s he’s wrong about is applying it to the earth, because of the vastly different rates of rotation, as I showed in my blog posts.
Roy wrote:
“My only point was that for the moon, with its slow rotation and with no atmosphere, you cannot compute the global average temperature from the global average absorbed solar flux.”
My calculation is over the full diurnal cycle, since it averages over the equatorial longitudes.
Radiative physics does not give the temperature of the dark side of the moon — that depends on the thermal conductance of the lunar regolith. I take that as a given constant, which the data show it mostly is.
All you need to do is apply the SB Law pointwise on the sunward size of the moon. Then add the backside constant.
I get exactly the right value for the equatorial average, exactly the right maximum, and and the exact shape of the curve along the lunar day hour.
http://davidappell.blogspot.com/2012/04/norfolk-constabulary-made-wrong-charges.html
Roy,
With regard to the statement in the text of your blog “the existence of water would lead to evaporation/sublimation, and a water vapour atmosphere. So an ice Earth is, I believe, incompatible with the assumption of no atmosphere. But Im open to different arguments on this point.”
Yes in the total absence of any atmospheric gases this has to be true. Any water vapour, no matter how tiny by sublimation/evaporation, would by definition make up 100% of the atmosphere.
However for those who dismiss the idea of an ice Earth, the situation would very different to what you described above, if the atmosphere was as it is at present with only the greenhouse gases absent.
Assuming -18C or -23 C temperatures, there would be very little water vapour in the atmosphere.
At 1 atmosphere pressure there would be next to no sublimation or evaporation of ice at these temperatures even in the presence of direct sunlight (heat of vapourization for water is 2,260 Kj/kg and the latent heat of fusion is 333 KJ/kg).
This is consistent with the desert like conditions in large parts of the Antarctica and in particular the water vapour data from the Antarctic. For integrated water vapour in the Antarctic , the reported values in winter are as low as 0.2 kg/m2 see http://tinyurl.com/j3j3du4 and http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.494.1598&rep=rep1&type=pdf. Similarly monthly mean precipitable water is about 0.4 mm see http://www.aeolus.wsu.edu/vonw/pubs/TownEtAl_2005.pdf .
re: MikeR says: October 2, 2016 at 6:59 AM
I made long post which didn’t post. In short there is
about “12,900 cubic kilometers” of water in our current atmosphere- 12.9 trillion tonnes. Were Earth to be -23 C
the would be several trillion tons of water in Earth atmosphere and most water in Earth atmosphere would be in the tropics. Or most water in atmosphere is currently in tropics
in colder world it would be an even greater difference.
Or in -23 C earth, there would as much water in atmosphere per square km average as compared to water per square km over say, Kansas on average. And the tropics on average would warmer than Kansas [but not as hot during summer and not as cold as during the winter].
Oh, one more thing, if one could throughly mix the Earth ocean, so surface ocean temperature were the average ocean temperature- earth would be about -20 C, until the surface waters warmed back up. Or average earth temperatures would steeply rise in the course of one year.
Where do you get that number? The global averge ocean temperature should be about 6 or 7 deg. C, as I recall.
wiki:
“Deep ocean water makes up about 90% of the volume of the oceans. Deep ocean water has a very low temperature, typically from 0-3 C (32-38 F), and a salinity of about 3.5% or as oceanographers state as 35 ppt (parts per thousand).”
https://en.wikipedia.org/wiki/Deep_ocean_water
But that does not fully account for number I gave.
And the number has various assumption- or I have a lot uncertainly about various kind of global weather effect. But mixing entire ocean would give real meaning to the term, climate change. It would have to effect the weather in Kansas- significantly.
In simple terms it’s knocking off 20 K off the tropical zone- until it warms up again. Or I doubt the global average temperature would remain near -20 C [15 C – 35 K] for an entire year- unless you continued to mixed the ocean for a year.
I am thinking there would a disappearance of clouds outside the tropical regions starting within days or weeks. That might not be true.
The tropics itself should have reduction in clouds and in it’s evaporation rate- or I think that given, but also think to effects could effect cloud formation outside the tropics and the clouds would sort of quickly “freeze out” or rain/snow out. And I think clouds outside the tropics cause a considerable amount of warming in terms of average temperature.
Or if clouds outside tropics were not effected much, then you will not get earth’s average temperature as low as -20 C. So I thinking of severe reduction in clouds globally- which will cause more clear skies in tropics, but it’s water would be cold from mixing and take some time before it’s surface warms enough warm air above it and to cause evaporation.
So right after entire ocean is mixed, tropics and everywhere
ocean surface temperature are 3 to 4 C in the daytime, and with clouds disappearing, and less water vapor, I would expect cooler air surface temperature at night- though that depends upon weather to some extent.
Average land temperature should plunge, but land temperatures don’t matter much with average global temperature- mixing ocean would temporally wipe out gulf stream- it not “just” turning off the gulf stream it’s making that ocean surface colder than without warm flow from tropics- or the only oceans you not cooling much are arctic oceans [or small portion of entire ocean]
So not going to get tropics or temperate zone ocean surface actually freezing, but the air above these oceans could get well below freezing during the night. And could see expansion of polar sea ice- though that is not very significant in terms of average global temperature.
So average global ocean air temperature of night and day could be could be less than 0 C maybe -5 C or colder.
So one has cold ocean surface.
Whereas warm oceans warm the land, these cold ocean don’t warm the land and may even make them cooler [maybe]. Making cooler as compare to ocean instead being land.
Or ocean absorb a lot of energy and is very slow to warm up.
Say the ocean were muddy, then oceans would be more like land surface- the top few inches could warm up quicker- so this couldn’t/wouldn’t cool the land. Though completely different way to say or look at this, is, the cool night air of land surface invades the ocean air.
But in simple terms, tropics warms the world, and with mixed ocean, the tropics stops warming the rest of the world- plus it’s likely a degree of weather chaos ensues- or could get average temperature of -20 C. But rather this is not global average trend this is a spike or spikes in temperatures in global average temperature- and could matter a bit when ocean are mixed in terms January or August.
Roy.
Do you have a reference for the 6 to 7 degree figures for the oceans?
A naive calculation with the land being 29% of the earths surface implies that land temperatures would be around – 95C to give an average global temperature of – 23C.
The – 95C land temperatures would make it much cooler than average temperature of Mars at – 55C. Does this sound reasonable?
Possibly the – 23C figure may not be appropriate in this case and water vapour is moderating things, but from the Antarctic data at these temperatures, there is not much about, especially above the land.
Sorry if duplicated
In order for Roys theory to be true then an experiment is required. Shine IR at a rotating sphere and measure the temperature for different rates of rotation. Common sense would say that the temperature was independent of the rate of rotation since the sphere absorbs as a circular cross section.
it seems you have spin a sphere is vacuum or air convectional
loss would increase the faster it’s spun
Notice how the daytime temperature profile is almost parabolic. Analogous to the convex parabolic reflector required to translate a parallel beam of light into spherical.
https://wattsupwiththat.files.wordpress.com/2012/01/lunar-surface-temperature1.jpg
Or I should say radial rather than spherical, i.e. a virtual point source.
Hi
Interesting reading. Should it be possible to test the hypothesis with a small solid sphere, and put it on a turntable and vary the speed?
Radiating it with a constant source, and measure the temperature at different RPM.